线性代数矩阵论——矩阵的分类
根据矩阵中包含元素的内容及分布排列形式,可将矩阵如下分类:
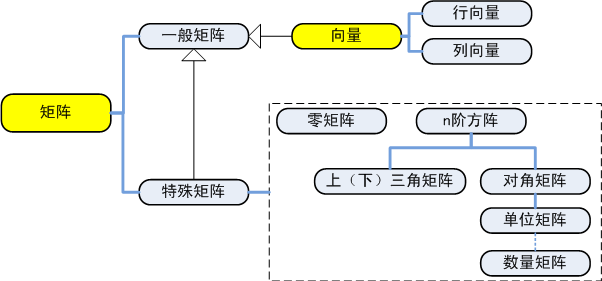
图1 按元素内容及排列形式的矩阵分类及各类矩阵之间的关系
一般矩阵
数域F上的m*n个数aij,i=1, 2, …, m; j=1, 2, …, n, 排成m行n列的数表
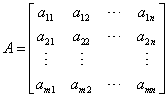 ,称为m*n矩阵,简记为A=[aij]m*n
,称为m*n矩阵,简记为A=[aij]m*n
零矩阵
所有元素都为0的矩阵。记为0
n阶方阵
行数与列数相等的矩阵。
对角矩阵
不在对角线上的元素皆为0的n阶方阵。记为
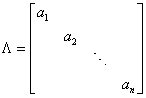
单位矩阵
主对角线上元素都为1,其余元素为0的n阶方阵。记为
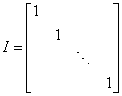
数量矩阵
主对角线上的元素等于同一个数k的对角矩阵。
上(下)三角矩阵
主对角线下(上)放元素皆为零的方阵。记为
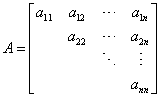 ,
,

行向量
m=1,即A中只有一行的矩阵。记为
列向量
n=1,即A中只有一列的矩阵。记为
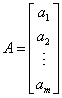
Matlab实现
一般矩阵:直接输入元素用空格或逗号隔开,用“;”表示一行的结束,并用[]将所有元素括起来。
较大的矩阵可以分成若干行输入,以回车键代替分号。
矩阵的元素可以是Matlab表达式。
用分号”;”附加一行或一个矩阵。
用冒号”:”从大矩阵中提取小矩阵。
用两重或多重省略号”……”表示续行
行向量和列向量为一般矩阵的特殊形式
零矩阵:zeros(m,n)
对角矩阵:diag([a1,a2,…,an])
单位矩阵:eye(m,n)
元素都为1的矩阵:ones(m,n)
参考文献:
[1] 刘先忠, 杨明. 线性代数. 北京: 高等教育出版社.