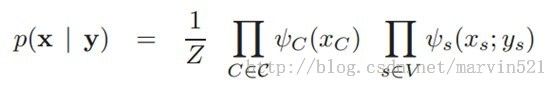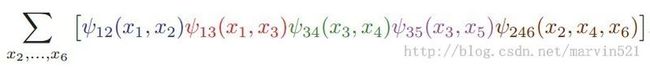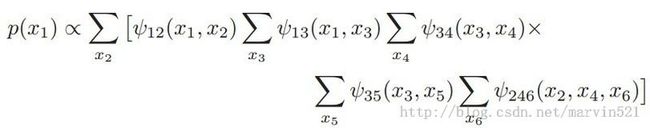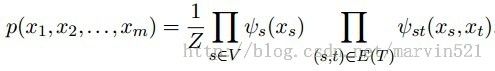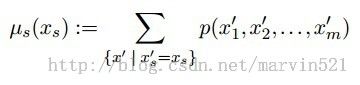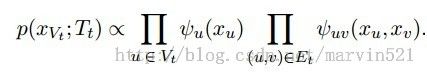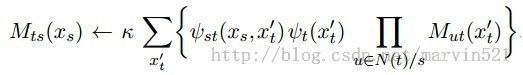机器学习理论与实战(十五)概率图模型03
03 图模型推理算法
这节了解一下概率图模型的推理算法(Inference algorithm),也就是如何求边缘概率(marginalization probability)。推理算法分两大类,第一类是准确推理(Exact Inference),第二类就是近似推理(Approximate Inference)。准确推理就是通过把分解的式子中的不相干的变量积分掉(离散的就是求和);由于有向图和无向图都是靠积分不相干变量来完成推理的,准确推理算法不区分有向图和无向图,这点也可以在准确推理算法:和积算法(sum-product)里体现出来,值得一提的是有向图必须是无环的,不然和积算法不好使用。如果有向图包含了环,那就要使用近似推理算法来求解,近似推理算法包含处理带环的和积算法(”loopy” sum-product)和朴素均值场算法(naive mean field),下面就来了解下这两种推理算法的工作原理。
假如给一个无向图,他包含数据节点X和标签Y,它可以分解成(公式一)的形式:
(公式一)
有些人一开始觉得(公式一)很奇怪,貌似和上一节的无向图分解有点不一样,其实是一样的,稍微有点不同的是把不同的团块区分对待了,这里有两种团块,比如(公式一)右边第一项是归一化常量配分函数,第二项可能是先验概率,而第二项就可能是给定标签时样本的概率。这里用可能这个措辞,表示这些势函数只是一个抽象的函数,他可以根据你的应用来变化,它就是对两种不同团块的度量。如果X的取值状态只有两个,那么配分函数可以写成(公式二)的形式:
(公式二)
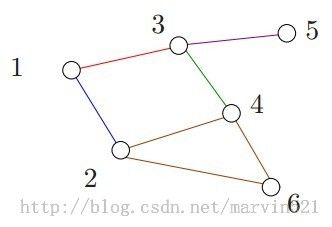
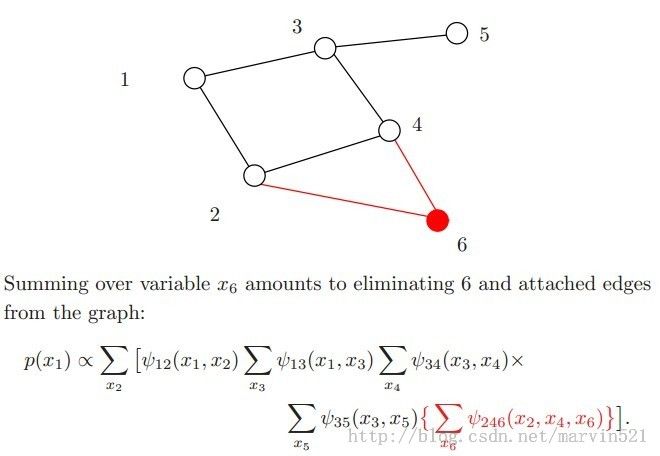
配分函数就是把所有变量都积分掉得到的最终的度量值,如果要求边缘概率就要通过积分掉其他变量得到的度量值除以配分函数,例如我们要求(图一)中的x1的边缘概率P(x1):
(图一)
要求取P(x1),我们就要积分掉x2-x6这五个变量,写成数学的形式如(公式三)所示:
(公式三)
如果你对代数分配率很熟悉,外面的加法符号大sigma可以分开写成(公式四)的样子:
(公式四)
其实(公式四)就是和积算法的雏形,因为可以很明显的看出又有和又有积。有些同学可能要问积分掉变量的顺序为什么是那样?其实这个没有准则的,先积分掉哪个变量,积分的顺序也会导致运算量大小不一样,求取最优的积分变量顺序是NP-hard的,下面用图示演示下积分消除变量发生的事情。
(01)
(02)
(03)
(04)
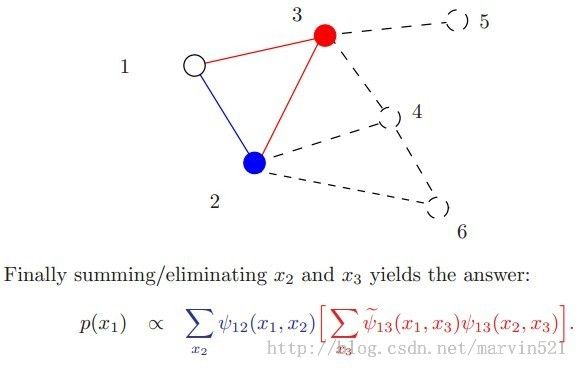
(05)
(图二)
(图二)中注意观察下每次积分掉一个变量后,原来的团块就因为少了一个变量变成了一个新的团块,新的团块使得图被三角剖分了,尤其在倒数第二个图更明显,消除变量x4后形成新的团块(x2,x3),使得x2,x3之间建立了一条连接(蓝线所示),这个三角化添加的边在图论里被成为弦(chord),全部完成三角化的图也称端正图(moral graph)。而边缘概率计算量的复杂度取决于剩下的变量形成的团块大小,如(图二)中红色的部分,变量消除的顺序也会影响新团块的大小,寻找一个最优的变量消除顺序十分必要,但是寻找最优的变量消除顺序是NP-hard的,眼看着问题就没法解决了,但如果图模型是树呢?树这种图模型具有良好的性质,他的计算量不大,下面先叉开下话题去看下树结构的图模型的边缘概率求解方法:
假设树结构的图模型如(图三)所示:
(图三)
和(公式一)类似,这个树结构的图模型的分布可以分解成(公式一)的形式,因为树可简单的分解成节点和边,那么它分解的形式如(公式五)所示:
(公式五)
把上面所述的和积算法写成一个通用的形式公式,如(公式六)所示:
(公式六)
这里注意下大sigma下标中的竖线表示排除Xs这个变量,积分掉其他变量,最终得到Xs的边缘概率。现在问题来了,在(图三)中,如果要求变量Xs的边缘概率就要积分掉Xs周围的其他四个变量(Xt,Xw,Xu,Xv),这是由(公式五)中的团块决定的(有边相连),而要积分掉这周围的四个变量就要继续积分掉这四个变量周围除Xs以外的其他相邻变量,这是个递归过程。而动态规划其实也是递归,所以本质上和积算法(sum-product)是个非连续的动态规划算法。下面用数学语言更进一步的梳理下这个递归算法流程,先做几个定义:
对于任意的属于V的节点变量s,它的临域可以定义成(公式七)的样子:
(公式七)
用 ![]() 表示和要计算边缘概率节点变量相连的子树,如变量s,但是子树不能越过变量s,如(图三)中的Tt,Tw,Tu,Tv都是子树,每个子树上的变量用
表示和要计算边缘概率节点变量相连的子树,如变量s,但是子树不能越过变量s,如(图三)中的Tt,Tw,Tu,Tv都是子树,每个子树上的变量用 ![]() 表示,那么每个子树又可以做团块分解,如(公式八)所示:
表示,那么每个子树又可以做团块分解,如(公式八)所示:
(公式八)
有了这些定义,我们就可以再重新梳理下刚才的递归过程,要计算变量Xs的边缘概率,就要计算其临域上的边缘概率,然后再临域的临域上的边缘概率,其实就是子树上的边缘概率,最终会递归到整个树的叶子节点上,叶子节点计算完成后传到父亲节点,以后依次向上传,最终传递到变量Xs上,这个过程其实叫消息传递(Message-Passing),有时也叫置信传播(BeliefPropagation),有了消息的概念,那(公式八)就可以变成(公式九)的样子:
(公式九)
(公式九)中k表示归一化常量,Mts表示从变量Xt传向Xs的消息,其实就是从子树上传递过来的,然后P表示子树的子树上传递过来的消息,引入消息的好处就是容易描述这个递归过程,另外也容易扩展到其他带环的图上,因为动态规划是递归的,递归用消息传播来表示,那么带环的图用消息传递的方法求解,我们就说其实用了动态规划算法,这个话题就不扯远了。
另外有了消息传播机制,上述的计算边缘概率的方法还可以扩展一下,使得可以同时计算所有节点的边缘概率,这就使得计算速度大大提高。我们可以让每个节点都同时沿着边向其临域传送消息,消息如(公式十)所示:
(公式十)
这样其实是传播了2倍于边数的消息,然后开始迭代,第二轮迭代时用第一轮传播来过来的子树上的消息更新当前消息,然后依次迭代下去,迭代n次后,消息值收敛,这样每个变量周围的消息都已确定,就不需要递归了,套用下(公式九)就可以计算边缘概率了。计算最大边缘概率(max-marginal)也是类似的方法,只不过是在收敛收选取最大的边缘概率而已,虽然简单,但是应用范围很广,因为很多时候都是在寻找个极值,比如立体匹配就是这个原理。
说完了树结构图模型的和积算法,就要回来说一般图的和积算法了,通过上面可以看到树结构的图模型具有容易计算的优点,那对于一般图模型如果能转成树也可以套用上面所述方法,我们可以把节点分组以团块的形式放在树的节点上,但是要注意连续性,因为一般图中的节点边可以很复杂,比如有环的图,那么一个节点变量就可以属于多个团块。因此团块树也要保持原有图的这种特性,不然求解不正确,因此团块树的定义就要来了,如(图四)所示:
(图四)
这段话不好翻译,也没见过中文对应的术语,因此只能直接贴图了,满足这种定义的团块树又称联合树,联合树其实就是说满足团块之间的连续性,每个相临团块之间都有公共变量,又成分割变量(separator-S),如(图五)的C图中的矩形所示:
(图五)
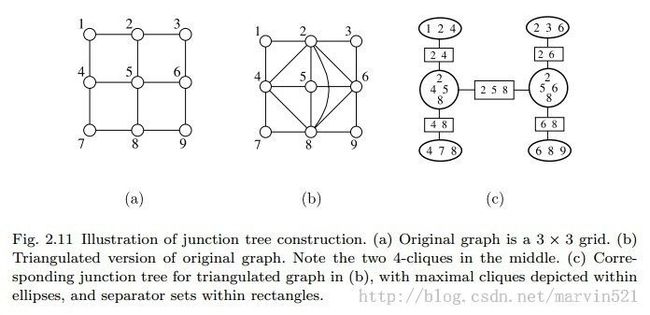
在(图五)中a图是有环的一般图模型,要想把a图转成联合树图,必须把其三角化,也就是说每三个变量围成一个环,多于3个的必须添加弦边,这其实是回应了上面最初的和积算法,Lauritzen在参考文献[3]中也对这种处理方法给出了证明,有兴趣的可以翻阅下。
对于一般图转联合树的步骤来个总结,如(图六)所示:
(图六)
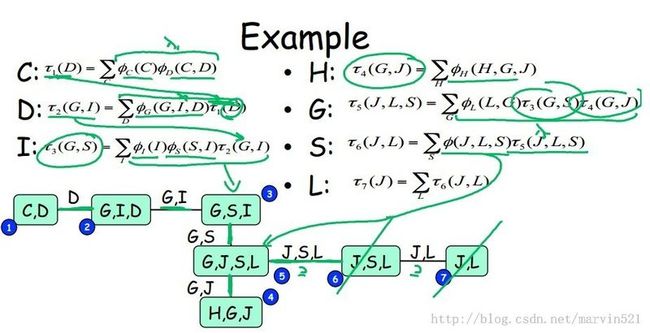
联合树建立后,就可以把树结构的消息传递算法推广到联合树上,树的节点由原来的单一变量变成了团块,那如何传递消息?其实也简单,每次传消息时积分掉和非公共变量的变量,然后用公共变量的消息传递就行了,如(图七)所示:
(图七)
(图七)中上半部分表示消息的内容,套用树结构消息传递方式,迭代收敛就行了,不过能否收敛还是一个值得深究的问题,今天就不展开了,理解联合树算法的核心就是理解消息到底是什么,看的很晕的就带着这个问题再看一遍咯^.^,另外逼近推理的变分方法需要用到极家族函数和凸分析来做统一框架,因此下节开始学习极家族函数。
参考文献:
[1] Graphical models, exponential families, and variational inference. Martin Wain wright and Michael Jordan
[2] Probabilistic Graphical Models. Daphne Koller
[3] Graphical Models.S. L. Lauritzen
转载请注明来源:http://blog.csdn.net/marvin521/article/details/10858655