时间复杂度和空间复杂度2 - 数据结构和算法04

时间复杂度和空间复杂度2

 

让编程改变世界

Change the world by program

---

 

算法时间复杂度

  我们说好的时间复杂度和空间复杂度呢？ 历来大学老师在讲解这两个概念，都是直接登堂入室，导致八成学生对概念理解不深刻，或者说只是硬背起来而已。   为了让大家能够更好地接受这两个比较重要的概念，我们有了上一讲的准备环节。 这一讲我们直接切入正题，介绍计算复杂度的攻略，然后通过一系列例子和大家一起分析总结规律。   算法时间复杂度的定义：在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。   算法的时间复杂度，也就是算法的时间量度，记作：T(n)= O(f(n))。 它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中f(n)是问题规模n的某个函数。   好长好长，没想到定义这个概念的老家伙比小甲鱼还罗嗦。（关键需要知道执行次数==时间） 这样用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。   一般情况下，随着输入规模n的增大，T(n)增长最慢的算法为最优算法。 显然，由此算法时间复杂度的定义可知，我们的三个求和算法的时间复杂度分别为O(1)，O(n)，O(n^2)。   三个求和算法？哪有？忘了？ 好吧，看看以下这张图能不能勾起点回忆？ [caption id="attachment_729" align="aligncenter" width="493"]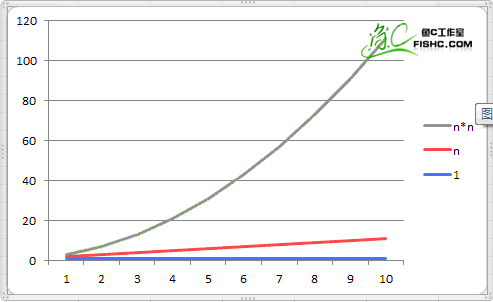 算法时间复杂度[/caption]  

推导大O阶方法

  那么如何分析一个算法的时间复杂度呢？即如何推导大O阶呢？  

我们给大家整理了以下攻略：

用常数1取代运行时间中的所有加法常数。 在修改后的运行次数函数中，只保留最高阶项。 如果最高阶项存在且不是1，则去除与这个项相乘的常数。 得到的最后结果就是大O阶。

  世界上的东西就是这么简单，老头儿们把它讲复杂，那么它就复杂了，举几个例子：  

常数阶

  [codesyntax lang="c"]

int sum = 0, n = 100;

printf(“I love fishc.comn”);
printf(“I love Fishc.comn”);
printf(“I love fishC.comn”);
printf(“I love fIshc.comn”);
printf(“I love FishC.comn”);
printf(“I love fishc.comn”);

sum = (1+n)*n/2;

[/codesyntax]   大家觉得这段代码的大O是多少？     O(8)？这是初学者常常犯的错误，总认为有多少条语句就有多少。 分析下，按照我们的概念“T(n)是关于问题规模n的函数”来说，这里大家表示对鱼C的爱固然是好的，要支持的，要鼓励的，要大力表彰的。   但是，跟问题规模有关系吗？没有，跟问题规模的表亲戚都没关系！，所以我们记作O(1)就可以。 另外，如果按照攻略来，那就更简单了，攻略第一条就说明了所有加法常数给他个O(1)即可。  

线性阶

  一般含有非嵌套循环涉及线性阶，线性阶就是随着问题规模n的扩大，对应计算次数呈直线增长。 [codesyntax lang="c"]

int i , n = 100, sum = 0;

for( i=0; i < n; i++ )
{
    sum = sum + i;
}

[/codesyntax]   上面这段代码，它的循环的时间复杂度为O(n)，因为循环体中的代码需要执行n次。  

平方阶

  刚才是单个循环结构，那么嵌套呢？ [codesyntax lang="c"]

int i, j, n = 100;

for( i=0; i < n; i++ )
{
    for( j=0; j < n; j++ )
    {
        printf(“I love FishC.comn”);
    }
}

[/codesyntax]   n等于100，也就是说外层循环每执行一次，内层循环就执行100次，那总共程序想要从这两个循环出来，需要执行100*100次，也就是n的平方。所以这段代码的时间复杂度为O(n^2)。   那如果有三个这样的嵌套循环呢？   没错，那就是n^3啦。所以我们很容易总结得出，循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。 刚刚我们每个循环的次数都是一样的，如果： [codesyntax lang="c"]

int i, j, n = 100;

for( i=0; i < n; i++ )
{
    for( j=i; j < n; j++ )
    {
        printf(“I love FishC.comn”);
    }
}

[/codesyntax]   惨了，老办法好像在这里套不上了，咋整？！ 分析下，由于当i=0时，内循环执行了n次，当i=1时，内循环则执行n-1次……当i=n-1时，内循环执行1次，所以总的执行次数应该是： n+(n-1)+(n-2)+…+1 = n(n+1)/2   大家还记得这个公式吧？恩恩，没错啦，就是搞死先生发明的算法丫。 那咱理解后可以继续，n(n+1)/2 = n^2/2+n/2 用我们推导大O的攻略，第一条忽略，因为没有常数相加。第二条只保留最高项，所以n/2这项去掉。第三条，去除与最高项相乘的常数，最终得O(n^2)。  

对数阶

  对数，属于高中数学内容啦，对于有些鱼油可能对这玩意不大理解，或者忘记了，也没事，咱分析的是程序为主，而不是数学为主，不怕。 我们看下这个程序： [codesyntax lang="c"]

int i = 1, n = 100;

while( i < n )
{
    i = i * 2;
}

[/codesyntax]   由于每次i*2之后，就举例n更近一步，假设有x个2相乘后大于或等于n，则会退出循环。 于是由2^x = n得到x = log(2)n，所以这个循环的时间复杂度为O(logn)。   其实理解大O推导不算难，难的是对数列的一些相关运算，这更多的是考察你的数学知识和能力。 所以这里小甲鱼要分两类来说下，对于想考研的朋友，需要强化一下你的数学尤其是数列方面的知识。 对于想增长自己编程能力的朋友，大概知道规律即可，不要在高等数学的概念上死磕！ [buy]? 获得所有教学视频、课件、源代码等资源打包?[/buy] [Downlink href='http://kuai.xunlei.com/d/LSFJEFWVZSAZ']视频下载[/Downlink] [Downlink href='http://urlxf.qq.com/?6VZzY3f']备胎下载[/Downlink]