经典算法题每日演练——第十题 树状数组
有一种数据结构是神奇的,神秘的,它展现了位运算与数组结合的神奇魅力,太牛逼的,它就是树状数组,这种数据结构不是神人是发现不了的。
一:概序
假如我现在有个需求,就是要频繁的求数组的前n项和,并且存在着数组中某些数字的频繁修改,那么我们该如何实现这样的需求?当然大家可以往
真实项目上靠一靠。
① 传统方法:根据索引修改为O(1),但是求前n项和为O(n)。
②空间换时间方法:我开一个数组sum[],sum[i]=a[1]+....+a[i],那么有点意思,求n项和为O(1),但是修改却成了O(N),这是因为我的Sum[i]中牵
涉的数据太多了,那么问题来了,我能不能在相应的sum[i]中只保存某些a[i]的值呢?好吧,下面我们看张图。
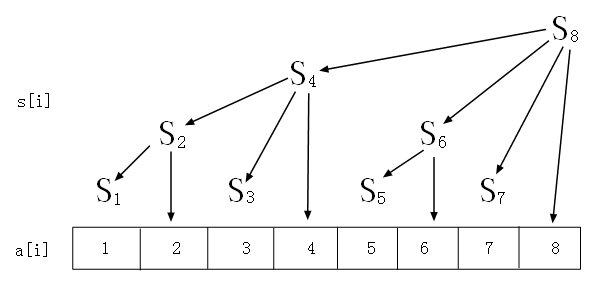
从图中我们可以看到S[]的分布变成了一颗树,有意思吧,下面我们看看S[i]中到底存放着哪些a[i]的值。
S[1]=a[1];
S[2]=a[1]+a[2];
S[3]=a[3];
S[4]=a[1]+a[2]+a[3]+a[4];
S[5]=a[5];
S[6]=a[5]+a[6];
S[7]=a[7];
S[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8];
之所以采用这样的分布方式,是因为我们使用的是这样的一个公式:S[i]=a[i-2k+1]+....+a[i]。
其中:2k 中的k表示当前S[i]在树中的层数,它的值就是i的二进制中末尾连续0的个数,2k也就是表示S[i]中包含了哪些a[],
举个例子: i=610=01102 ;可以发现末尾连续的0有一个,即k=1,则说明S[6]是在树中的第二层,并且S[6]中有21项,随后我们求出了起始项:
a[6-21+1]=a[5],但是在编码中求出k的值还是有点麻烦的,所以我们采用更灵巧的Lowbit技术,即:2k=i&-i 。
则:S[6]=a[6-21+1]=a[6-(6&-6)+1]=a[5]+a[6]。
二:代码
1:神奇的Lowbit函数
1 #region 当前的sum数列的起始下标
2 /// <summary>
3 /// 当前的sum数列的起始下标
4 /// </summary>
5 /// <param name="i"></param>
6 /// <returns></returns>
7 public static int Lowbit(int i)
8 {
9 return i & -i;
10 }
11 #endregion
2:求前n项和
比如上图中,如何求Sum(6),很显然Sum(6)=S4+S6,那么如何寻找S4呢?即找到6以前的所有最大子树,很显然这个求和的复杂度为logN。
1 #region 求前n项和
2 /// <summary>
3 /// 求前n项和
4 /// </summary>
5 /// <param name="x"></param>
6 /// <returns></returns>
7 public static int Sum(int x)
8 {
9 int ans = 0;
10
11 var i = x;
12
13 while (i > 0)
14 {
15 ans += sumArray[i - 1];
16
17 //当前项的最大子树
18 i -= Lowbit(i);
19 }
20
21 return ans;
22 }
23 #endregion
3:修改
如上图中,如果我修改了a[5]的值,那么包含a[5]的S[5],S[6],S[8]的区间值都需要同步修改,我们看到只要沿着S[5]一直回溯到根即可,
同样它的时间复杂度也为logN。
1 public static void Modify(int x, int newValue)
2 {
3 //拿出原数组的值
4 var oldValue = arr[x];
5
6 for (int i = x; i < arr.Length; i += Lowbit(i + 1))
7 {
8 //减去老值,换一个新值
9 sumArray[i] = sumArray[i] - oldValue + newValue;
10 }
11 }
最后上总的代码:
 View Code
View Code
1 using System;
2 using System.Collections.Generic;
3 using System.Linq;
4 using System.Text;
5 using System.Diagnostics;
6 using System.Threading;
7 using System.IO;
8
9 namespace ConsoleApplication2
10 {
11 public class Program
12 {
13 static int[] sumArray = new int[8];
14
15 static int[] arr = new int[8];
16
17 public static void Main()
18 {
19 Init();
20
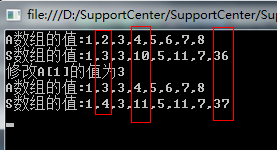
21 Console.WriteLine("A数组的值:{0}", string.Join(",", arr));
22 Console.WriteLine("S数组的值:{0}", string.Join(",", sumArray));
23
24 Console.WriteLine("修改A[1]的值为3");
25 Modify(1, 3);
26
27 Console.WriteLine("A数组的值:{0}", string.Join(",", arr));
28 Console.WriteLine("S数组的值:{0}", string.Join(",", sumArray));
29
30 Console.Read();
31 }
32
33 #region 初始化两个数组
34 /// <summary>
35 /// 初始化两个数组
36 /// </summary>
37 public static void Init()
38 {
39 for (int i = 1; i <= 8; i++)
40 {
41 arr[i - 1] = i;
42
43 //设置其实坐标:i=1开始
44 int start = (i - Lowbit(i));
45
46 var sum = 0;
47
48 while (start < i)
49 {
50 sum += arr[start];
51
52 start++;
53 }
54
55 sumArray[i - 1] = sum;
56 }
57 }
58 #endregion
59
60 public static void Modify(int x, int newValue)
61 {
62 //拿出原数组的值
63 var oldValue = arr[x];
64
65 arr[x] = newValue;
66
67 for (int i = x; i < arr.Length; i += Lowbit(i + 1))
68 {
69 //减去老值,换一个新值
70 sumArray[i] = sumArray[i] - oldValue + newValue;
71 }
72 }
73
74 #region 求前n项和
75 /// <summary>
76 /// 求前n项和
77 /// </summary>
78 /// <param name="x"></param>
79 /// <returns></returns>
80 public static int Sum(int x)
81 {
82 int ans = 0;
83
84 var i = x;
85
86 while (i > 0)
87 {
88 ans += sumArray[i - 1];
89
90 //当前项的最大子树
91 i -= Lowbit(i);
92 }
93
94 return ans;
95 }
96 #endregion
97
98 #region 当前的sum数列的起始下标
99 /// <summary>
100 /// 当前的sum数列的起始下标
101 /// </summary>
102 /// <param name="i"></param>
103 /// <returns></returns>
104 public static int Lowbit(int i)
105 {
106 return i & -i;
107 }
108 #endregion
109 }
110 }
 View Code
View Code