关于GDAL计算图像坐标的几个问题

使用GDAL处理地理图像时，不可避免的会遇到一个问题，图像的地理坐标问题，因为有了这个地理坐标，地理图像才和普通图像有了最本质的区别，那么在使用GDAL时，如果处理与地理坐标相关的信息呢？下面进行简单的说明。

1：如何使用行列号计算图像的地理坐标？或者如何通过地理坐标来定位在图像的某个位置？

2：如何获取图像的四至范围？或者如果通过指定的地理范围计算图像的所在区域？

要解决上面三个问题，首先需要知道和了解GDAL的数据模型，其中里面有个非常重要的就是投影和六参数。这两个可以使用GDALDataset类中的GeoTransform()函数和GetProjectionRef()函数来进行获取。第一个参数获取的是图像的六参数（我自己起的名字，是一个仿射变化的参数），第二个是图像的投影（也就是空间参考系统）。下面先说说第一个六参数，六参数其实是图像行列号坐标和地理坐标转换的一组转换系数。下面是用GT来表示六参数，图像行列号与图像的地理坐标之间的数学关系式如下：

 

    Xgeo = GT(0) + Xpixel*GT(1) + Yline*GT(2)
    Ygeo = GT(3) + Xpixel*GT(4) + Yline*GT(5)

上式中，Xgeo和Ygeo表示的图像的地理坐标，Xpixel表示图像的列号，Yline表示图像的行号，GT(i)就是上面所说的六参数，一共是六个值。这六个值大致可以分为三组，GT(0)和GT(3)是第一组，表示图像左上角的地理坐标；GT(1)和GT(5)是第二组，表示图像横向和纵向的分辨率（一般这两者的值相等，符号相反，横向分辨率为正数，纵向分辨率为负数）；GT(2)和GT(4)是第三组，表示图像旋转系数，对于一般图像来说，这两个值都为0。

 

为什么说图像的GT(0)和GT(3)表示图像左上角的坐标，对于图像行列号坐标系统来说，坐标的原点在左上角，所以左上角的行列号是(0,0)，将坐标带入上式，可以得到：

 

    Xgeo = GT(0)
    Ygeo = GT(3)

所以说GT(0)和GT(3)表示图像左上角的坐标。

 

GT(1)和GT(5)表示图像横向和纵向的分辨率。图像的分辨率就是图像每个像素所能表示的面积，一般都是正方形的格网，所以也就是没两个相邻像元坐标的差值。基于这个原理，使用两个坐标进行验证。假设当前点行列号坐标为A（i，j），相邻的右侧点坐标为B（i+1，j）。分别计算A和B的横向地理坐标，并计算差值，即：

dX = XgeoB - XgeoA = [GT(0) + (i+1)*GT(1) + j*GT(2)] - [GT(0) + i*GT(1) + j*GT(2)] =  GT(0) -GT(0) + (i+1)*GT(1) - i*GT(1) + j*GT(2) - j*GT(2) =  (i+1)*GT(1) - i*GT(1) = GT(1)

同理可以得到 dY= GT(5)。

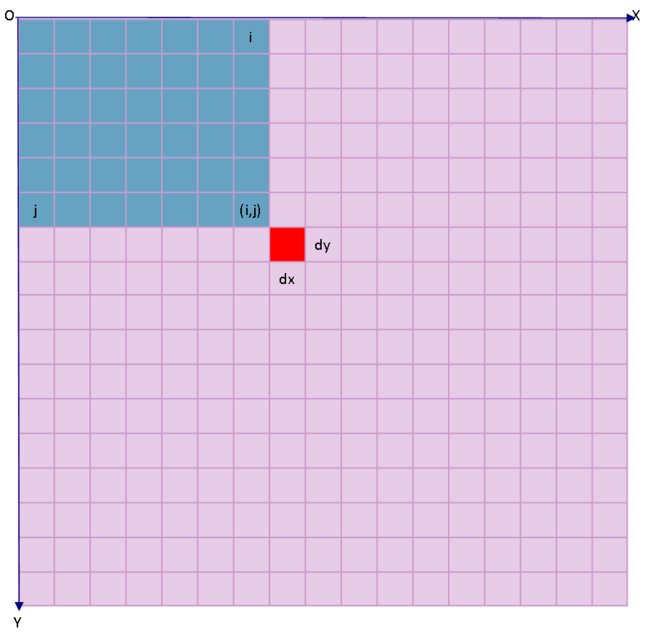
对于一个普通的标准图像来说（这里的标准图像是指GT(2)和GT(4)都为0），如图1所示，图像的行列号坐标为XOY，每个网格代表一个图像像素区域，i表示列号，j表示行号，淡蓝色右下角的行列坐标为（i，j），图中红色方块纵向长度为dy，横向长度为dx，分别为图像的分辨率；图中O点的地理坐标就是（GT(0),GT(3)）。

图1 一个标准的图像行列号坐标及其地理坐标说明

有了上面的说明，那么就可以很简单的来进行图像的行列号与地理坐标进行相互转换，具体的代码如下，共有两个，一个正算，一个反算。

 

bool Projection2ImageRowCol(double *adfGeoTransform, double dProjX, double dProjY, int &iCol, int &iRow)
{
	try
	{
		double dTemp = adfGeoTransform[1]*adfGeoTransform[5] - adfGeoTransform[2]*adfGeoTransform[4];
		double dCol = 0.0, dRow = 0.0;
		dCol = (adfGeoTransform[5]*(dProjX - adfGeoTransform[0]) - 
			adfGeoTransform[2]*(dProjY - adfGeoTransform[3])) / dTemp + 0.5;
		dRow = (adfGeoTransform[1]*(dProjY - adfGeoTransform[3]) - 
			adfGeoTransform[4]*(dProjX - adfGeoTransform[0])) / dTemp + 0.5;

		iCol = static_cast<int>(dCol);
		iRow = static_cast<int>(dRow);
		return true;
	}
	catch(...)
	{
		return false;
	}
}

bool ImageRowCol2Projection(double *adfGeoTransform, int iCol, int iRow, double &dProjX, double &dProjY)
{
	//adfGeoTransform[6]  数组adfGeoTransform保存的是仿射变换中的一些参数，分别含义见下
	//adfGeoTransform[0]  左上角x坐标 
	//adfGeoTransform[1]  东西方向分辨率
	//adfGeoTransform[2]  旋转角度, 0表示图像 "北方朝上"
	//adfGeoTransform[3]  左上角y坐标 
	//adfGeoTransform[4]  旋转角度, 0表示图像 "北方朝上"
	//adfGeoTransform[5]  南北方向分辨率

	try
	{
		dProjX = adfGeoTransform[0] + adfGeoTransform[1] * iCol + adfGeoTransform[2] * iRow;
		dProjY = adfGeoTransform[3] + adfGeoTransform[4] * iCol + adfGeoTransform[5] * iRow;
		return true;
	}
	catch(...)
	{
		return false;
	}
}

现在我们再回到之前开头的两个问题。对于第一个问题，实际就是图像行列号坐标与地理坐标的相互转换，上面的代码就可以用来解决。对于第二个问题，可以转换为第一个问题，第二个问题其实就是两个点的坐标转换，分别是左上角点和右下角点。比如第一个，如何计算图像的四至范围，图像的四至范围从图1中可以看出，图像的四至其实就是图像左上角坐标和右下角的坐标为起来的矩形区域，那么就分别将左上角和右下角的行列号按照上面的公式进行转换即可得到四至范围；对与第二问就是将这个坐标进行反算得到。

 

关于地理图像的坐标问题就说到这里，关于上面的投影信息（空间参考信息），需要说明一下，这个六参数里面的坐标范围是和空间参考是一一对应的，比如空间参考是一个WGS84椭球体，那么这个六参数一般的单位就是度，如果是北京54等分带投影，那么六参数的单位就是米。