谈到单根区间上方程求根的近似算法,我们第一印象就是高中的时候接触的二分法,正如其名称,二分法就是通过每次把f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值。
大概步骤如下:
假定f(x)在区间(x,y)上连续
先找到a、b属于区间(x,y),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2],
现在假设f(a)<0,f(b)>0,a<b
①如果f[(a+b)/2]=0,该点就是零点,
②如果f[(a+b)/2]<0,则在区间((a+b)/2,b)内有零点,(a+b)/2>a,从①开始继续使用中点函数值判断。
③如果f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2<b,从①开始继续使用中点函数值判断。
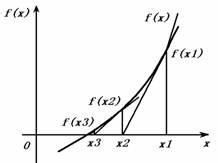
此外还有另外一种方法,叫牛顿迭代法,也称牛顿切线法,它也是一种近似算法,内容如下:
设r是f(x)=0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y=f(x)的切线L,L的方程为y=f(x0) f'(x0)(x-x0),求出L与x轴交点的横坐标 x1=x0-f(x0)/f'(x0),称x1为r的一次近似值,如果|f(x1)-0|小于指定的精度,那么继续过点(x1,f(x1))做曲线y=f(x)的切线,并求该切线与x轴的横坐标 x2=x1-f(x1)/f'(x1)称x2为r的二次近似值,重复以上过程。得r的近似值序列{Xn},其中Xn 1=Xn-f(Xn)/f'(Xn),称为r的n 1次近似值。上式称为牛顿迭代公式。
现用matlab编写两种方法,比较它们的收敛速度。
1.先给出需要求根函数:
function f=cal(x) f=exp(-0.005*x)*cos(sqrt(2000-0.01*x*x)*0.05)-0.01; end2.二分法函数:
function [xvalue,gap,fx,count]=bisect(a,b,nmax,eps,fun)
% xvalue--自变量迭代值 gap--区间长度 fx--函数值 count--计数
% nma--所允许执行的最大次数,防止死循环 eps--允许的误差 fun--调用的函数名
err=eps+1;
count=0;%初始化计数值为0
xvalue=[];%xvalue向量存储变量x的值
gap=[];%gap向量存储误差值
fx=[];%fx向量存储函数值
while(err>eps&&count<nmax)
%当误差err大于所给的误差长度或者计数小于允许运行次数时,执行算法
count=count+1;%计数加1
c=(a+b)/2;%计算中间值
x=c;
xvalue=[xvalue;x];%将自变量迭代值存入xvalue矩阵
fc=feval(fun,x);%将自变量代入cal函数得到的函数值赋给fc
fx=[fx;fc];%将fc函数值存入fx矩阵
x=a;
%判断根在哪个区域
if(fc*feval(fun,x)<0)
b=c;
else
a=c;
end
err=abs(b-a);%误差长度
gap=[gap;err];
end
disp(' 次数 自变量 区间长 函数值 ')
%输出相应数据
for i=1:count
fprintf('%2d %10.6f %10.6f %10.6f \n ',i,xvalue(i),gap(i),fx(i))
end
3.牛顿迭代法函数:
function [xvalue gap fx,count]=Newton(x0,nmax,eps,fname)
%初始化xvalue,gap,fx向量
xvalue=[];
gap=[];
fx=[];
count=0;%初始化计数为0
x1=x0+1;
m=eps+1;
while(m>eps&&count<nmax)
count=count+1;%计数
f=feval(fname,x0);%得到f(x0)函数值
xvalue=[xvalue;x0];
fx=[fx;f];
x1=x0-f/df(x0);
gap=[gap;x1-x0];
m=abs(x1-x0);
x0=x1;%x1传值给x0,准备进行下一次迭代
end
disp('次数 自变量 区间长 函数值 ')
%输出数据
for i=1:count
fprintf('%2d %10.6f %10.6f %10.6f \n',i,xvalue(i),gap(i),fx(i))
end 4.牛顿迭代法中需要用的求导函数:
function h=df(x) %求函数的导函数 syms R %符号化R y=cal(R);%调用cal函数 dy=diff(y);%求cal函数的导函数 h=subs(dy,R,x);%获得cal函数的导函数取x的值 end5.脚本:
%分别调用二分法和牛顿迭代法
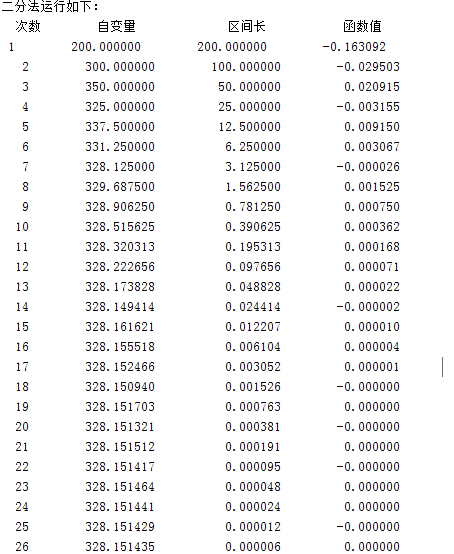
disp('二分法运行如下:')
bisect(0,400,50,0.000001,@cal);
disp(' ')
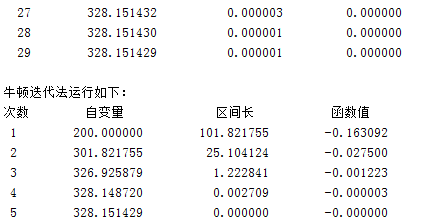
disp('牛顿迭代法运行如下:')
Newton(200,50,0.000001,@cal);