数据挖掘导论学习笔记(2)----- 数据(3)
相似性和相异性的度量
相似度:两个对象之间的相似度(similarity) 的非正式定义是这两个对象相似程度的数值度量。因而,两个对象越相似,它们的相似度越高。通常,相似度是非负的,并常常在0(不相似)和(完全相似)之间取值。
相异度:两个对象之间的相异度是这两个对象差异程度的数值度量。对象越相似,它们的相异度就越低。通常,术语距离(distance)用作相异度的同义词。有时,在区间【0,1】中取值,但在0和∞之间取值也很常见
本节,我们介绍广泛用于计算数值属性刻画的对象的相异性的距离度量。这些度量包括欧几里得距离、曼哈顿距离和闵可夫斯基距离。
在某些情况下,在计算距离之前数据应该规范化。这涉及变换数据,使之落入较小的公共值域,如[-1,1]或[0.0,1.0]。例如,考虑 height(高度)属性,它可能用米或英寸测量。一般而言,用较小的单位表示一个属性将导致该属性具有较大的值域,因而趋向于给这种属性更大的影响或 “权重”。规范化数据试图给所有属性相同的权重。在特定的应用中,这可能有用,也可能没用。数据规范化方法在第3章数据预处理中详细讨论。
最流行的距离度量是欧几里得距离(即,直线或“乌鸦飞行”距离)。令i=(xi1,xi2,…,xip)和j=(xj1,xj2,…,xjp)是两个被p个数值属性描述的对象。对象i和j之间的欧几里得距离定义为:
另一个著名的度量方法是曼哈顿(或城市块)距离,之所以如此命名,是因为它是城市两点之间的街区距离(如,向南2个街区,横过3个街区,共计5个街区)。其定义如下:
![]()
欧几里得距离和曼哈顿距离都满足如下数学性质:
非负性:d(i,j)≥0:距离是一个非负的数值。
同一性:d(i,i)=0:对象到自身的距离为0。
三角不等式:d(i,j)≤d(i,k)+d(k,j):从对象i到对象j的直接距离不会大于途经任何其他对象k的距离。
满足这些条件的测度称做度量(metric)1 。注意非负性被其他三个性质所蕴含。
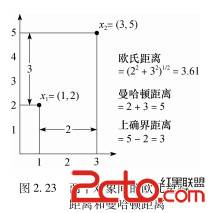
例2.19 欧几里得距离和曼哈顿距离。令x1=(1,2)和x2=(3,5)表示如图2.23所示的两个对象。两点间的欧几里得距离是![]() 。两者的曼哈顿距离是2+3=5。
。两者的曼哈顿距离是2+3=5。
闵可夫斯基距离(Minkowski distance)是欧几里得距离和曼哈顿距离的推广 ,定义如下:
其中,h是实数,h≥1。(在某些文献中,这种距离又称Lp范数(norm),其中p就是我们的h。我们保留p作为属性数,以便于本章的其余部分一致。)当p=1时,它表示曼哈顿距离(即,L1范数);当p=2表示欧几里得距离(即,L2范数)。
上确界距离(又称Lmax,L∞范数和切比雪夫(Chebyshev)距离)是h→∞时闵可夫斯基距离的推广 。为了计算它,我们找出属性f,它产生两个对象的最大值差。这个差是上确界距离,更形式化地定义为:
L∞范数又称一致范数(uniform norm)。
例2.20 上确界距离。让我们使用相同的数据对象x1=(1,2)和x2=(3,5),如图2.23所示。第二个属性给出这两个对象的最大值差为5-2=3。这是这两个对象间的上确界距离。
如果对每个变量根据其重要性赋予一个权重,则加权的欧几里得距离可以用下式计算:
![]()
加权也可以用于其他距离度量。
_________________________________________________________
1 在数学文献,特别是在测度论中,measure被译为“测度”,metric被译为“度量”。在计算机科学文献中,metric很少用,而 measure通常译为“度量”。仅当measure和metric同时出现时,我们才按照数学的习惯翻译,而在其他情况下,我们采用计算机科学的传统译 法。——译者注
二元数据的相似度
1.SMC(Simple Matching Coefficient 简单匹配系统树)
2.Jaccard系数(Jaccard Coefficient)
3.余弦相似度
4.广义Jaccard系数
5.皮尔森相关
6.Bregman三度