哈夫曼树的初始化,编码,译码及横向打印
哈夫曼树介绍:(好吧,部分copy自百度知道^_^)
哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为WPL=(W1*L1+W2*L2+W3*L3+...+ Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
利用哈夫曼编码进行通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或子孙结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
4、哈夫曼编码
在数据通信中,需要将传送的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。例如,需传送的报文为“AFTER DATA EAR ARE ART AREA”,这里用到的字符集为“A,E,R,T,F,D”,各字母出现的次数为{8,4,5,3,1,1}。现要求为这些字母设计编码。要区别6个字母,最简单的二进制编码方式是等长编码,固定采用3位二进制,可分别用000、001、010、011、100、101对“A,E,R,T,F,D”进行编码发送,当对方接收报文时再按照三位一分进行译码。显然编码的长度取决报文中不同字符的个数。若报文中可能出现26个不同字符,则固定编码长度为5。然而,传送报文时总是希望总长度尽可能短。在实际应用中,各个字符的出现频度或使用次数是不相同的,如A、B、C的使用频率远远高于X、Y、Z,自然会想到设计编码时,让使用频率高的用短码,使用频率低的用长码,以优化整个报文编码。
5、哈夫曼译码
在通信中,若将字符用哈夫曼编码形式发送出去,对方接收到编码后,将编码还原成字符的过程,称为哈夫曼译码。
问题描述:
利用哈夫曼编码进行通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。但是,这要求在发送端通过一个编码系统对待传数据预先编码,在接受端将传来的数据进行译码(复原)。对于双工信道(即可以双向传输信息的信道),每端都需要一个完整的编/译码系统。试为这样的信息收发站写一个哈夫曼码的编/译码系统。
功能实现及算法简要分析(C语言实现):(这个是完全原创滴,拷贝到VC下可直接运行。大家多多指教^_^图是用win下的画图画的哈)
1,索引源文件。
读取原文并统计字符个数和每个字符的出现次数即权值,存入自定义类型data型数组中。data的数据结构定义:
typedef struct{
char c; //字符内容
int num; //字符出现次数即权值
int code[31]; //字符的2进制编码
int co_n; //2进制编码的长度
}Data;
2,初始化哈夫曼树。
根据字符的权值建立哈夫曼树。先看哈夫曼树节点的数据结构定义:
typedef struct{
Data *leaf; //指向Data类型的叶子节点内容的指针,若此节点不是叶子节点,此指针为NULL
int weight; //权值或子节点weight值的集合
int parent; //双亲节点的下标
int lchild; //左孩子的下标
int rchild; //又孩子的下标
}HuTree;
哈夫曼树为方便起见,通过数组保存,通过下标访问各个节点。
假设第一步中统计出的字符个数为c_num,则叶子节点个数为c_num,总结点数为2*num-1。(因为在哈夫曼树中不存在度数为1的节点,根据二叉树的性质,节点度数为2的节点数为叶子节点数减1)
初始化树的基本思路是:
1)对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,..., Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。
2)在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
3)从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
4)重复2)和3),直到集合F中只有一棵二叉树为止。
e.g:
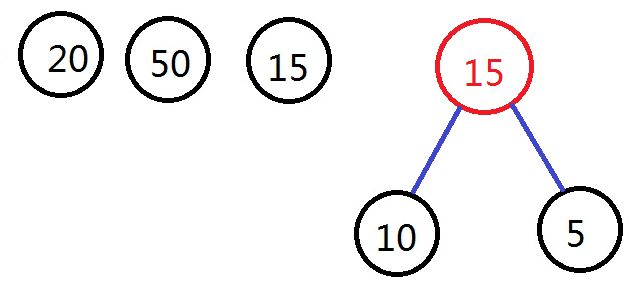
通过select函数从从中选择出两个权值最小的节点,即权值为10和5的节点,构成新的二叉树,根节点权值为15,加入到集合F中,从集合F中删去10和5的节点。如图所示:
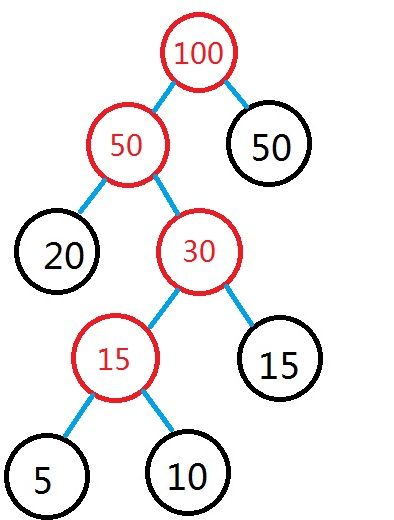
 以此类推,直到集合F中只有一个树为止,此树即为建成的哈夫曼树。如图所示:
以此类推,直到集合F中只有一个树为止,此树即为建成的哈夫曼树。如图所示:
自此建树完成。其中根节点的下标为2*c_num-1。下面是完整的建树代码:
3,哈夫曼编码
编码的思路是,先找到要编码的字符所在的结点,然后按它的parent域找到双亲结点,判断前一结点是此双亲结点的左孩子还是有孩子,前者将0写入暂时的code[]数组,并将域co_n加一。如此往复,直到结点的parent域为0。然后逆转数组。
注意在main函数中要按之前索引到的字符数循环调用此函数,实现所有字符的编码。之后要将编码写入到code.txt文件中,算法不再啰嗦。如下:
4,哈夫曼译码
译码需要先读入保存01码的文件,设整形curr指向当前在ht[]中的位置,初始化指向2*c_num-1,即根结点。然后依次读入01码,若为0,则将curr指向原结点的左孩子,若为2,则将curr指向右孩子。以此往复,直到curr指向结点的leaf域不为NULL,即是叶子结点时。然后将此叶子节点指向的Data类型的c域内容打印到控制台,并写入到TestFile.txt文件中。然后重置curr指向根结点,继续读码,直到code文件读完返回EOF为止。若此时curr没有指向叶子节点,则说明2进制的编码有问题。代码如下:
5,哈夫曼树的横向打印
使用逆中序法遍历哈夫曼树,加入适当的改变即可打印,由于与哈夫曼树的算法关系不大,不解释,你懂的^_^。代码如下:
最后打印出来带有类似表格的效果,比较好辨认。
6,Main函数
这个就是用switch搞的一个简单控制台界面,包括调用各个函数,不详述。代码如下:
7,说明
之上是所有的代码分开写。其中完全展开的是比较重要的算法,不是很重要的为滚动条。其中建树的算法、译码的算法(主要是文件操作上的问题)、横向打印哈夫曼树的算法花费了比较多的时间调试、找bug。其它的算法基本上是一气呵成的,呵呵。大家注意下,哈!下面附上完整代码。
HuTree.h
Main.c