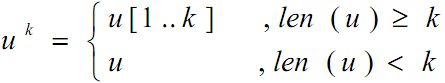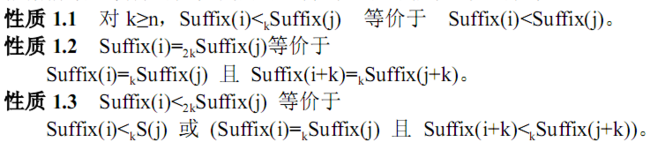后缀数组
一、后缀数组 及其对应的名次数组
举例:S=" B A C $ " , 后缀数组长度为n-1= 3 , 假定'$'<字符集Σ中的任意字符
1 2 3 4
1. 后缀数组SA=[4 2 1 3] , 对应所有后缀的一个字典序 从小到大的序列
SA[1]=4 --> 对应 "$"
SA[2]=2 --> 对应 "A C $"
SA[3]=1 --> 对应 "B A C $"
SA[4]=3 --> 对应 "C $"
2. 名次数组Rank=SA^-1, 方便地查询每个后缀在后缀数组中的名次
Rank[4]=1 --> Suffix(4)="$" 在后缀数组中排第1
Rank[2]=2 --> Suffix(2)="A C $" 在后缀数组中排第2
Rank[1]=3 --> Suffix(1)="B A C $" 在后缀数组中排第3
Rank[3]=4 --> Suffix(3)="C $" 在后缀数组中排第4
一、构造后缀数组——“k-前缀比较”的倍增方法(Doubling Algorithm)
1. k-前缀
A. 性质1.2、 1.3 使得我可以倍增的重排:
“1-前缀排序”的前缀数组SA_1[]=Suffix(i)...
“2-前缀排序”的前缀数组SA_2[]=Suffix(i)...
“4-前缀排序”的前缀数组SA_4[]=Suffix(i)...
“8-前缀排序”的前缀数组SA_8[]=Suffix(i)...
...
“k-前缀排序”的前缀数组SA_k[]=Suffix(i)...
注: 所有SA_i中的元素都是一样的(字符串的所有可能后缀),只不过排列顺序不同
B. 性质1.1 当k≥n时,“字典顺序” 和 “k-前缀顺序”就是一个东东了!
告诉我们当k≥n时,就可以结束了:) 因为此时SA_k[]中后缀顺序即是“所有后缀按照字典顺序的排列”了。
3. 基于k-前缀的构造后缀数组(及其名次数组)
初始化:
从 “1-前缀 前缀数组SA_1” 开始;
计算出她对应的 “1-前缀 名次数组Rank_1” ; //O(n)时间 (Rank=SA^-1)
while(k<n){
//O(nlogn)时间,
// A. “2k-前缀比较”Suffix_2k(i)和Suffix_2k(j)用时O(1)
// B. 从小到大快排所有Suffix_2k(i)用时O(nlogn)(注:大小比较是=2k, <2k这样的“2k-前缀比较”)
性质2.3,用“k-前缀 前缀数组SA_k” 和 “k-前缀 名次数组Rank_k” 构造 “2k-前缀 前缀数组SA_2k” ;
//O(n)时间 (Rank=SA^-1)
计算 “2k-前缀 前缀数组SA_2k” 对应的 “2k-前缀 名次数组Rank_2k” ;
}
三、height[]数组 height[i]=lcp( Suffix(SA[i-1]), Suffix(SA[i]) )
区别和明确几个定义: lcp(u,v)和LCP(i,j); height[]和h[]的定义:
(1)任意两个字符串的“最长公共前缀长度 ”: lcp(u,v) = max{i | u =i v}, =i表示“i-前缀等于”关系
int lcp(String u, String v);
(2)后缀数组中两个元素对应字符串的“最长公共前缀长度 ”:LCP(i,j) = lcp( Suffix(SA[i]), Suffix(SA[j]) )
int LCP(int i, int j);
注意:i和j是在后缀数组SA[]中的排名/位置 ,不对应原字符串中后缀的开始位置;
SA[i]和SA[j]才对应了这两个后缀 开始的字符 在原字符串中的位置 。
LCP Theorem :
设i<j,则LCP(i,j) = min{ LCP(k-1,k) | i+1≤k≤j } = min{ height[i+1], height[i+2], ... , height[j] }
(3)后缀数组中“第i-1个元素”和“第i个元素”的“最长公共前缀长度 ”
height[i] = LCP(i-1, i) = lcp( Suffix(SA[i-1]), Suffix(SA[i]) )
(4)原字符串中“从位置i开始的后缀”和“该后缀在SA[]中前一个元素(另一个后缀)”的“ 最长公共前缀长度 ”
h[i] = height[ Rank[i] ] = height[Rank[i]-1, Rank[i]] = lcp( Suffix(Rank[i]-1), Suffix(Rank[i]) )
注意:
(1)
height[i]中i 含义是 “目标后缀是后缀数组SA[]中的第i个元素/SA[]中排名第i的元素/字典序第i小的元素”
h[i]中的i 含义是 “目标后缀是从原字符串中位置i开始的后缀S[i, ..., n]”. 令,原字符串为S[1, ..., n]
(2)数组名称总是代表函数值的含义
sa[排名]=后缀字符串
rank[后缀字符串]=排名
模板代码:我的这个模板改造了罗穗骞的代码,使之更容易理解![]()
/////////////////////////////////////////////////////////////////
//Constructing Suffix Array with Doubling Algorithm
//Constructing Height[]
/////////////////////////////////////////////////////////////////
#include <algorithm>//sort
#include <cstring>//memset
#include <iostream>
using namespace std;
const int MAX_SFX = 210000;
struct Sfx {
//i --> 后缀在“原数组”中的位置(唯一确定了一个后缀字符串)
int i;
//key[0] --> 后缀S[i,...,n]在 “k-前缀排序”中的位置
//key[1] --> 后缀S[i+k,...,n]在“k-前缀排序”中的位置
int key[2];
bool operator < (const Sfx& s) const //后面的const是什么意思???
{
return key[0] < s.key[0]
|| (key[0] == s.key[0] && key[1] < s.key[1]);
}
};
int g_buf[MAX_SFX + 1];
Sfx g_tempSfx[2][MAX_SFX];
Sfx *g_sa = g_tempSfx[0]; //后缀数组 g_sa[0]~g_sa[len-1]
int rank[MAX_SFX]; //名次数组 rank[0]~rank[len-1]
int height[MAX_SFX]; //height数组 height[0]~height[len-1]. 注:包括 height[0](==0)
/*
CALL: cSort(in, len, key∈{0,1}, out);
EFFECT: in[0]~in[len-1],按照域 in[i].key[key]进行排序,结果放入out中
理解基数排序:
假设有4个字母 in[]={A B B A},即,有2个A;有2个B.
即,有2个≤A ;有4个≤B
现在按照字母顺序放置这4个字母 in[]={A B B A}
方法:
cnt[A]=2
cnt[B]=4
out[--cnt[B]]=B, 即out[--4]=B,即 out[3]=B
out[--cnt[B]]=B, 即out[--3]=B,即 out[2]=B
out[--cnt[A]]=A, 即out[--2]=A,即 out[1]=A
out[--cnt[A]]=A, 即out[--1]=A,即 out[0]=A
*/
void cSort(Sfx* in, int n, int key, Sfx* out) {
//cnt[]: cnt[i]表示 in[i].key[1]的值≤i的 in[i]的个数
int* cnt = g_buf;
memset( cnt, 0, sizeof(int) * (n + 1) );
for (int i = 0; i < n; i++){
cnt[ in[i].key[key] ]++;
}
for (int i = 1; i <= n; i++){
cnt[i] += cnt[i - 1];
}
for (int i = n - 1; i >= 0; i--){
//输入元素数组中的元素 in[i] 应该放到输出数组中的位置 out[...]
out[ --cnt[ in[i].key[key] ] ] = in[i];
}
}
/*
Build a suffix array from string 'text' whose length is 'len'.
write the result into global array 'g_sa'.
*/
void buildSA(char* text, int len) {
Sfx *temp = g_tempSfx[1];
int* rank = g_buf;
//1. g_sa[]中后缀数组按照 1-前缀关系从小到大排列
for (int i = 0; i < len; i++){
g_sa[i].i = i;
g_sa[i].key[0] = text[i];
g_sa[i].key[1] = i; //这句省略后结果相同
}
sort(g_sa, g_sa + len);
for (int i = 0; i < len; i++) {
g_sa[i].key[1] = 0;
}
//2. 每次循环计算 “k-前缀关系 名次数组” 和 “2k-前缀关系 后缀数组”
int k = 1;
while (k < len) {
//2.1 计算 “k-前缀关系 名次数组”
//计算 k-前缀关系名次数组rank[]前,g_sa[]已经按照 k-前缀关系 ↑排序了
rank[ g_sa[0].i ] = 1;
for (int i = 1; i < len; i++){
rank[ g_sa[i].i ] = rank[ g_sa[i - 1].i ];
if( g_sa[i-1] < g_sa[i] ){
rank[ g_sa[i].i ]++;
}
}
//2.2 计算 “2k-前缀关系 后缀数组”
// 2.2.A 设置了g_sa[]中每个元素的 i, key[0], key[1]三个域
for (int i = 0; i < len; i++){
g_sa[i].i = i; //i --> 后缀在“原数组”中的位置(唯一确定了一个后缀字符串)
g_sa[i].key[0] = rank[i]; //key[0] --> 后缀S[i,...,n]在 “k-前缀排序”中的位置
g_sa[i].key[1] = i + k < len? rank[i + k]: 0; //key[1] --> 后缀S[i+k,...,n]在“k-前缀排序”中的位置
}
// 2.2.B 根据 key[0], key[1]两个域,从小到大排列 g_sa[]中的每个元素
cSort(g_sa, len, 1, temp);
cSort(temp, len, 0, g_sa);
k *= 2;
}
}
/*
Build height[]
注:朴素算法计算height[]需要 O(n^2); 这里采用罗穗骞的算法,按照h[i]的顺序计算,时间复杂度为O(n)
*/
void buildHeight(char* str, Sfx* sa, int len){
//构造名次数组
for(int i=0; i<len; i++)
rank[ sa[i].i ] = i;
//按照 h[1], h[2], ... , h[n]的顺序计算,即按照 height[ rank[1] ], height[ rank[2] ],...顺序计算
//这样计算h[]的累积时间为O(n)
// h[]定义:h[i] = height[ rank[i] ]
// h[]性质:h[i] >= h[i-1]-1 有点像单调增:不会大退步
int k=0;
for(int i=0; i<len; i++){
//此刻, k==h[i-1]
if(k>0) k--;
//此刻,k==h[i-1]-1
//j: 后缀数组中排在Suffix(i)前一位的后缀的位置
int j=sa[ rank[i]-1 ].i;
//h[i]≥h[i-1]-1 == k, 只需将 k从 h[i-1]增长到 h[i]即可
while(str[i+k]==str[j+k])
k++;
//相当于计算 h[i],因为height[rank[i]] = h[i]
height[ rank[i] ] = k;
}
}
int main() {
/* 字符串尾部填充'\0',(int)'\0'为0,小于所有字符的值*/
char str[] = "aabbaaababab";
buildSA(str, 13);
buildHeight(str, g_sa, 13);
//The first suffix is useless (empty).
for (int i=0; i<13; i++){
cout
<<g_sa[i].i
<<' '<<str+g_sa[i].i
<<' '<<height[i]
<<endl;
}
system("pause");
return 0;
}
四、后缀数组的应用
1. 最长公共前缀
对于j, k,则有(我起的名)“最长公共前缀性质 ”:
Suffix(j)和Suffix(k)是同一个字符串的两个后缀 。,不妨设rank[j]<rank[k],则Suffix(j)和Suffix(k)的最长公共前缀为height[rank[j]+1], height[rank[j]+2], height[rank[j]+3], ... , height[rank[k]]中的最小值。这样就可以用RMQ问题的几种解法(线段树/ST算法)。
2. 单个字符串相关问题
例一、给定一个字符串,求最长重复子串
解法:O(n): 查找height[]中最大元素值
例二、给定一个字符串,求最长不重叠重复子串
解法:
什么是不重叠最长子串呢,就是一个串中至少出现两次,又不重叠的子串中的最长的,比较绕口。
解决这个问题的关键还是利用height 数组。把排序后的后缀分成若干组,其中每组的后缀之间的height 值都不小于k。然后找出各个组的后缀的sa值的最大最小值max,min,如果存在 max-min >= k,那么就存在长度为k的不重叠子串,因为根据LCP定理,每个组中的height值都不小于k,就是说这个组中这些后缀的最长公共前驱最小是k,然后由于max-min>= k,所以可以判定存在所要求的子串。做题的时候二分答案,把问题变为判定性问题(大牛说的)。那么整个事件复杂度为O(nlogn)。把height数组分组的思想非常常用,可以多看看IOI论文了解了解。
(1)把题目变成判定性问题“判断是否存在两个长度≥k的两个相同子串,且不重叠”。将后缀数组分为若干组。其中后缀之间height值≥k的后缀在同一组,显然只有这样的组才可能出现长度≥k的两个相同子串,且不重叠。
(2)对于满足上述要求的组判断每个后缀的sa值的最大值和最小值之差是否≥k(≥k则不重叠)。
注:基于这个问题的扩展见POJ 1743 Musical Theme 传说中楼教主男人八题之一。
例三、给定一个字符串,求至少出现k次的最长重复子串(这k个子串可以重叠)???
例四、子串的个数——给定一个字符串,求不相同的子串的个数???