Matlab任意正六边形随机撒点 实现-----------通信仿真必备

任意正六边形随机撒点 是通信仿真里经常用到的，无奈网上资料很少，参照http://www.ilovematlab.cn/thread-136761-1-1.html，我又苦思敏想里一下午，这个问题才得以完美解决。废话不多说了，先来看看怎么画正六边形。

theta = linspace(0,2*pi,7);

plot(cos(theta),sin(theta),'g-');

两句代码就可以画出一个正六边形了，其中第一句也可以这样写：N=6;
theta = 0:2*pi/N:2*pi;

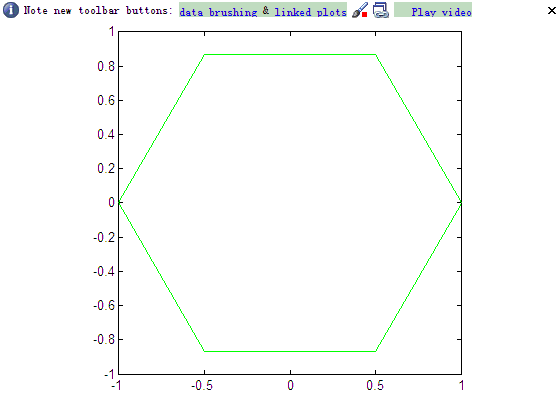
效果是一样的，无非是通过【cos（theta），sin（theta）】计算出七个点，将这七个点首尾依次相连，画出六条边。

如下图所示：

这个正六边形有点小特殊，它的中心在坐标轴的原点（0,0）处，边长d=1.网上还有另外一种画正六边的方法，是通过给顶中心O和边长d来计算出每个顶点的位置，用一个for循环画六次，相当麻烦，我未采用。但这种两句话画出的正六边形相当特殊，不能满足使用需要，用这种计算cos、sin得到点坐标的画法，网上再无资料了，怎么用这种画法画出任意中心O，边长d的正六变形呢？先来看我们把边长弄为d。首先看下面的图：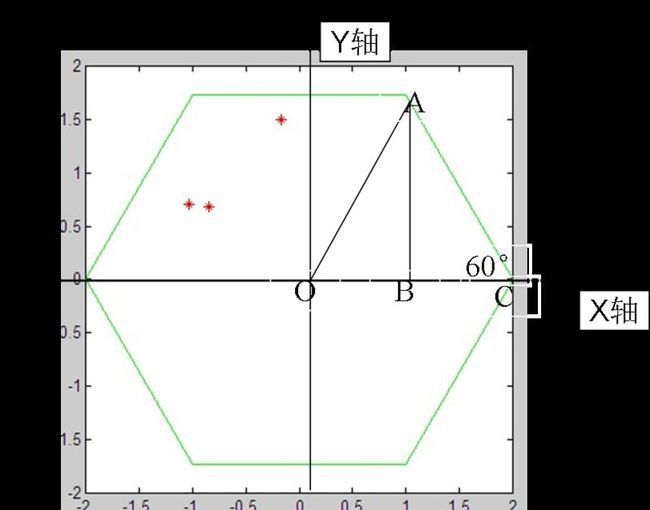

当边长为1时，正六边形最右边的点C坐标为（cos（0），sin（0）），也就是（1,0），当边长为d时C的坐标变成（d，0），通过计算不难发现A点的坐标变成（d/2, 根号3 *d），也就是（d*cos（theta）， d*sin（theta））。所以画出边长为d的正六边形程序改为：

N=6;
theta = 0:2*pi/N:2*pi;
D=1;
plot(D*cos(theta),D*sin(theta),'g-');就可以了，D是边长。假设我们的正六边形中心点P(x,y),而现在的中心在坐标原点O（0,0），两者构成一个向量PO（x，y）。所谓的d*cos(theta),d*sin(theta)算的其实就是六个顶点的坐标，将这些坐标按向量PO平移，得到平移后的6个顶点坐标为：d*cos（theta）+x， d*sin（theta）+y。因此画出边长为D，中心坐标为P（X，Y）的正六边形，程序可以这样写：

theta = linspace(0,2*pi,7);
D=2; %边长
X=1; %中心横坐标
Y=2; %中心纵坐标
plot(Dcos(theta)+X,D*sin(theta) + Y,'g-');这远比那个for循环来循环去的方法简单吧！

随机撒点问题：

首先看这里是往咱们画的第一个正六边形里撒一百个随机点的程序：

%%

theta = linspace(0,2*pi,7);

plot(cos(theta),sin(theta),'g-');

axis square

i = 0;

while i < 100

x = 2*rand(1,2)-1;

if (abs(x(1)) + abs(x(2))/sqrt(3) ) <= 1 && abs(x(2)) <= sqrt(3)/2

i = i+1;

hold on

plot(x(1),x(2),'r*');

end

end

hold off
这里i是撒点的个数。我们要彻底搞懂这个程序。我们先将这个程序扩展为边长为d的情况。x = 2*rand(1,2)-1;这句话是为了将随机点的横纵坐标锁定在[-1, 1]（这是正六变形的最左点和最右点）,当边长为d时，这句话变为：x =2*d*rand(1,2)-d

最让人蛋疼的是if (abs(x(1)) + abs(x(2))/sqrt(3) ) <= 1 && abs(x(2)) <= sqrt(3)/2 这句话，足足让我想了一个下午！显然这是为了给随机点加限制，保证随机点在正六边形内。这里x（1）是横坐标，x（2）是纵坐标。abs(x(2)) <= sqrt(3)/2，先看这句。在第一象限内，随机点纵坐标的值应该小于第二个图中AB的距离，当边长为d，而AB的最大值 = d*sqrt(3)/2.

另外一个条件abs(x(1)) + abs(x(2))/sqrt(3) ) <= 1。我们这样想，随机点最边界的情况就是在正六边形的边上，在第一象限为例，当随机点在边AC上时，OB+BC=1，为了和随机点的横纵坐标联系起来，这么写：OB + AB/tan(60) = 1, 边长为d时，边长OB + AB/tan(60) = d，所以临界条件是：OB + AB/tan(60) <= d.

假设中心点坐标为P（x，y），则随机点的坐标也要平移。平移后的坐标变成x（1） + x， x（2） + y，至此大功告成！最终的程序如下，如果需要连续在多个正六边形随机撒点，则要多次调用x = 2*D*rand(1,2)-1*D;
if (abs(x(1)) + abs(x(2))/sqrt(3) ) <= D && abs(x(2)) <= D*sqrt(3)/2，这样就能保证每次撒的随机点一定是随机的，且相互无影响。
大家可以根据需要把程序封装成函数调用：

%%
theta = linspace(0,2*pi,7);
D=2; %边长
X=1; %中心横坐标
Y=2; %中心纵坐标
plot(D*cos(theta)+X,D*sin(theta) + Y,'g-');
axis square


i = 0;
while i < 3
x = 2*D*rand(1,2)-1*D;
if (abs(x(1)) + abs(x(2))/sqrt(3) ) <= D && abs(x(2)) <= D*sqrt(3)/2
i = i+1;
hold on
plot(x(1) + X, x(2) + Y,'r*');
end
end
hold off

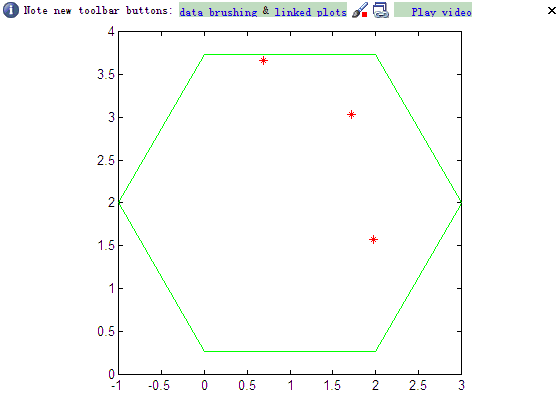
上面程序画出的图：

这里我们先找到边长为D，中心在（0， 0）时的撒出的随机点，然后通过向量平移plot(x(1) + X, x(2) + Y,'r*')画出中心在（X， Y）时的随机点， 哈哈，高一学的数学还真是有用啊！计算那个不等式关系好像是初三几何里，怀念我的老师们 和 那段难忘的日子！