Manacher算法

1.Manacher算法原理与实现

下面介绍Manacher算法的原理与步骤。

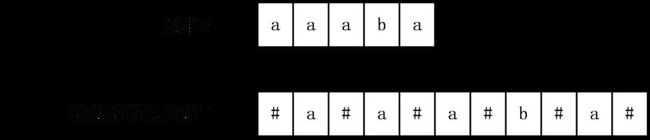
首先，Manacher算法提供了一种巧妙地办法，将长度为奇数的回文串和长度为偶数的回文串一起考虑，具体做法是，在原字符串的每个相邻两个字符中间插入一个分隔符，同时在首尾也要添加一个分隔符，分隔符的要求是不在原串中出现，一般情况下可以用#号。下面举一个例子：

（1）Len数组简介与性质

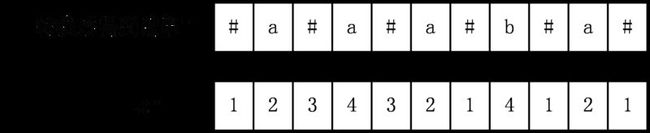
Manacher算法用一个辅助数组Len[i]表示以字符T[i]为中心的最长回文字串的最右字符到T[i]的长度，比如以T[i]为中心的最长回文字串是T[l,r],那么Len[i]=r-i+1。

对于上面的例子，可以得出Len[i]数组为:

Len 数组有一个性质，那就是Len[i]-1就是该回文子串在原字符串S中的长度，至于证明，首先在转换得到的字符串T中，所有的回文字串的长度都为奇数，那 么对于以T[i]为中心的最长回文字串，其长度就为2*Len[i]-1,经过观察可知，T中所有的回文子串，其中分隔符的数量一定比其他字符的数量多 1，也就是有Len[i]个分隔符，剩下Len[i]-1个字符来自原字符串，所以该回文串在原字符串中的长度就为Len[i]-1。

有了这个性质，那么原问题就转化为求所有的Len[i]。下面介绍如何在线性时间复杂度内求出所有的Len。

回到顶部

（2）Len数组的计算

首先从左往右依次计算Len[i]，当计算Len[i]时，Len[j](0<=j<i)已经计算完毕。设P为之前计算中最长回文子串的右端点的最大值，并且设取得这个最大值的位置为po，分两种情况：

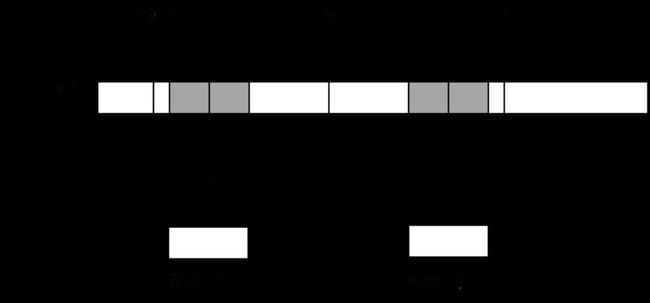
第一种情况：i<=P

那么找到i相对于po的对称位置，设为j，那么如果Len[j]<P-i，如下图：

那 么说明以j为中心的回文串一定在以po为中心的回文串的内部，且j和i关于位置po对称，由回文串的定义可知，一个回文串反过来还是一个回文串，所以以i 为中心的回文串的长度至少和以j为中心的回文串一样，即Len[i]>=Len[j]。因为Len[j]<P-i,所以说i+Len[j]& lt;P。由对称性可知Len[i]=Len[j]。

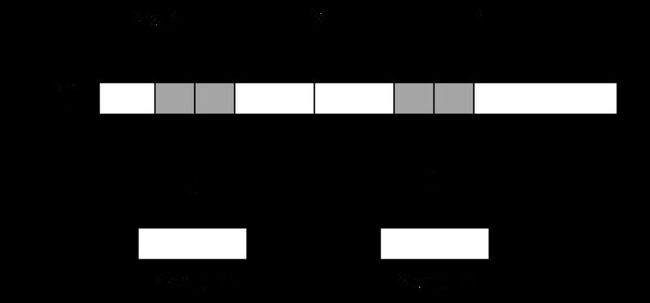
如果Len[j]>=P-i,由对称性，说明以i为中心的回文串可能会延伸到P之外，而大于P的部分我们还没有进行匹配，所以要从P+1位置开始一个一个进行匹配，直到发生失配，从而更新P和对应的po以及Len[i]。

第二种情况: i>P

如果i比P还要大，说明对于中点为i的回文串还一点都没有匹配，这个时候，就只能老老实实地一个一个匹配了，匹配完成后要更新P的位置和对应的po以及Len[i]。

2.时间复杂度分析

Manacher 算法的时间复杂度分析和Z算法类似，因为算法只有遇到还没有匹配的位置时才进行匹配，已经匹配过的位置不再进行匹配，所以对于T字符串中的每一个位置，只 进行一次匹配，所以Manacher算法的总体时间复杂度为O(n)，其中n为T字符串的长度，由于T的长度事实上是S的两倍，所以时间复杂度依然是线性 的。

下面是算法的实现，注意，为了避免更新P的时候导致越界，我们在字符串T的前增加一个特殊字符，比如说‘$’,所以算法中字符串是从1开始的。

const int maxn=1000010; 
char str[maxn];//原字符串 
char tmp[maxn<<1];//转换后的字符串 
int Len[maxn<<1]; 
//转换原始串 
int INIT(char *st) 
{ 
    int i,len=strlen(st); 
    tmp[0]='@';//字符串开头增加一个特殊字符，防止越界 
    for(i=1;i<=2*len;i+=2) 
    { 
        tmp[i]='#'; 
        tmp[i+1]=st[i/2]; 
    } 
    tmp[2*len+1]='#'; 
    tmp[2*len+2]='$';//字符串结尾加一个字符，防止越界 
    tmp[2*len+3]=0; 
    return 2*len+1;//返回转换字符串的长度 
} 
//Manacher算法计算过程 
int MANACHER(char *st,int len) 
{ 
     int mx=0,ans=0,po=0;//mx即为当前计算回文串最右边字符的最大值 
     for(int i=1;i<=len;i++) 
     { 
         if(mx>i) 
         Len[i]=min(mx-i,Len[2*po-i]);//在Len[j]和mx-i中取个小 
         else 
         Len[i]=1;//如果i>=mx，要从头开始匹配 
         while(st[i-Len[i]]==st[i+Len[i]]) 
         Len[i]++; 
         if(Len[i]+i>mx)//若新计算的回文串右端点位置大于mx，要更新po和mx的值 
         { 
             mx=Len[i]+i; 
             po=i; 
         } 
         ans=max(ans,Len[i]); 
     } 
     return ans-1;//返回Len[i]中的最大值-1即为原串的最长回文子串额长度  
  }