遗传算法解决TSP问题
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法
遗传算法的基本运算过程如下:
a)初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0)。
b)个体评价:计算群体P(t)中各个个体的适应度。
c)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。
d)交叉运算:将交叉算子作用于群体。所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。遗传算法中起核心作用的就是交叉算子。
e)变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。
群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t 1)。
f)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
下面用C语言模拟遗传算法模拟TSP问题
TSP问题及旅行商问题,假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define cities 10 //城市的个数
#define MAXX 100//迭代次数
#define pc 0.8 //交配概率
#define pm 0.05 //变异概率
#define num 10//种群的大小
int bestsolution;//最优染色体
int distance[cities][cities];//城市之间的距离
struct group //染色体的结构
{
int city[cities];//城市的顺序
int adapt;//适应度
double p;//在种群中的幸存概率
}group[num],grouptemp[num];
//随机产生cities个城市之间的相互距离
void init()
{
int i,j;
memset(distance,0,sizeof(distance));
srand((unsigned)time(NULL));
for(i=0;i<cities;i++)
{
for(j=i+1;j<cities;j++)
{
distance[i][j]=rand()%100;
distance[j][i]=distance[i][j];
}
}
//打印距离矩阵
printf("城市的距离矩阵如下\n");
for(i=0;i<cities;i++)
{
for(j=0;j<cities;j++)
printf("%4d",distance[i][j]);
printf("\n");
}
}
//随机产生初试群
void groupproduce()
{
int i,j,t,k,flag;
for(i=0;i<num;i++) //初始化
for(j=0;j<cities;j++)
group[i].city[j]=-1;
srand((unsigned)time(NULL));
for(i=0;i<num;i++)
{
//产生10个不相同的数字
for(j=0;j<cities;)
{
t=rand()%cities;
flag=1;
for(k=0;k<j;k++)
{
if(group[i].city[k]==t)
{
flag=0;
break;
}
}
if(flag)
{
group[i].city[j]=t;
j++;
}
}
}
//打印种群基因
printf("初始的种群\n");
for(i=0;i<num;i++)
{
for(j=0;j<cities;j++)
printf("%4d",group[i].city[j]);
printf("\n");
}
}
//评价函数,找出最优染色体
void pingjia()
{
int i,j;
int n1,n2;
int sumdistance,biggestsum=0;
double biggestp=0;
for(i=0;i<num;i++)
{
sumdistance=0;
for(j=1;j<cities;j++)
{
n1=group[i].city[j-1];
n2=group[i].city[j];
sumdistance+=distance[n1][n2];
}
group[i].adapt=sumdistance; //每条染色体的路径总和
biggestsum+=sumdistance; //种群的总路径
}
//计算染色体的幸存能力,路劲越短生存概率越大
for(i=0;i<num;i++)
{
group[i].p=1-(double)group[i].adapt/(double)biggestsum;
biggestp+=group[i].p;
}
for(i=0;i<num;i++)
group[i].p=group[i].p/biggestp; //在种群中的幸存概率,总和为1
//求最佳路劲
bestsolution=0;
for(i=0;i<num;i++)
if(group[i].p>group[bestsolution].p)
bestsolution=i;
//打印适应度
for(i=0;i<num;i++)
printf("染色体%d的路径之和与生存概率分别为%4d %.4f\n",i,group[i].adapt,group[i].p);
printf("当前种群的最优染色体是%d号染色体\n",bestsolution);
}
//选择
void xuanze()
{
int i,j,temp;
double gradient[num];//梯度概率
double xuanze[num];//选择染色体的随机概率
int xuan[num];//选择了的染色体
//初始化梯度概率
for(i=0;i<num;i++)
{
gradient[i]=0.0;
xuanze[i]=0.0;
}
gradient[0]=group[0].p;
for(i=1;i<num;i++)
gradient[i]=gradient[i-1]+group[i].p;
srand((unsigned)time(NULL));
//随机产生染色体的存活概率
for(i=0;i<num;i++)
{
xuanze[i]=(rand()%100);
xuanze[i]/=100;
}
//选择能生存的染色体
for(i=0;i<num;i++)
{
for(j=0;j<num;j++)
{
if(xuanze[i]<gradient[j])
{
xuan[i]=j; //第i个位置存放第j个染色体
break;
}
}
}
//拷贝种群
for(i=0;i<num;i++)
{
grouptemp[i].adapt=group[i].adapt;
grouptemp[i].p=group[i].p;
for(j=0;j<cities;j++)
grouptemp[i].city[j]=group[i].city[j];
}
//数据更新
for(i=0;i<num;i++)
{
temp=xuan[i];
group[i].adapt=grouptemp[temp].adapt;
group[i].p=grouptemp[temp].p;
for(j=0;j<cities;j++)
group[i].city[j]=grouptemp[temp].city[j];
}
//用于测试
/*
printf("<------------------------------->\n");
for(i=0;i<num;i++)
{
for(j=0;j<cities;j++)
printf("%4d",group[i].city[j]);
printf("\n");
printf("染色体%d的路径之和与生存概率分别为%4d %.4f\n",i,group[i].adapt,group[i].p);
}
*/
}
//交配,对每个染色体产生交配概率,满足交配率的染色体进行交配
void jiaopei()
{
int i,j,k,kk;
int t;//参与交配的染色体的个数
int point1,point2,temp;//交配断点
int pointnum;
int temp1,temp2;
int map1[cities],map2[cities];
double jiaopeip[num];//染色体的交配概率
int jiaopeiflag[num];//染色体的可交配情况
for(i=0;i<num;i++)//初始化
jiaopeiflag[i]=0;
//随机产生交配概率
srand((unsigned)time(NULL));
for(i=0;i<num;i++)
{
jiaopeip[i]=(rand()%100);
jiaopeip[i]/=100;
}
//确定可以交配的染色体
t=0;
for(i=0;i<num;i++)
{
if(jiaopeip[i]<pc)
{
jiaopeiflag[i]=1;
t++;
}
}
t=t/2*2;//t必须为偶数
//产生t/2个0-9交配断点
srand((unsigned)time(NULL));
temp1=0;
//temp1号染色体和temp2染色体交配
for(i=0;i<t/2;i++)
{
point1=rand()%cities;
point2=rand()%cities;
for(j=temp1;j<num;j++)
if(jiaopeiflag[j]==1)
{
temp1=j;
break;
}
for(j=temp1+1;j<num;j++)
if(jiaopeiflag[j]==1)
{
temp2=j;
break;
}
//进行基因交配
if(point1>point2) //保证point1<=point2
{
temp=point1;
point1=point2;
point2=temp;
}
memset(map1,-1,sizeof(map1));
memset(map2,-1,sizeof(map2));
//断点之间的基因产生映射
for(k=point1;k<=point2;k++)
{
map1[group[temp1].city[k]]=group[temp2].city[k];
map2[group[temp2].city[k]]=group[temp1].city[k];
}
//断点两边的基因互换
for(k=0;k<point1;k++)
{
temp=group[temp1].city[k];
group[temp1].city[k]=group[temp2].city[k];
group[temp2].city[k]=temp;
}
for(k=point2+1;k<cities;k++)
{
temp=group[temp1].city[k];
group[temp1].city[k]=group[temp2].city[k];
group[temp2].city[k]=temp;
}
//处理产生的冲突基因
for(k=0;k<point1;k++)
{
for(kk=point1;kk<=point2;kk++)
if(group[temp1].city[k]==group[temp1].city[kk])
{
group[temp1].city[k]=map1[group[temp1].city[k]];
break;
}
}
for(k=point2+1;k<cities;k++)
{
for(kk=point1;kk<=point2;kk++)
if(group[temp1].city[k]==group[temp1].city[kk])
{
group[temp1].city[k]=map1[group[temp1].city[k]];
break;
}
}
for(k=0;k<point1;k++)
{
for(kk=point1;kk<=point2;kk++)
if(group[temp2].city[k]==group[temp2].city[kk])
{
group[temp2].city[k]=map2[group[temp2].city[k]];
break;
}
}
for(k=point2+1;k<cities;k++)
{
for(kk=point1;kk<=point2;kk++)
if(group[temp2].city[k]==group[temp2].city[kk])
{
group[temp2].city[k]=map2[group[temp2].city[k]];
break;
}
}
temp1=temp2+1;
}
}
//变异
void bianyi()
{
int i,j;
int t;
int temp1,temp2,point;
double bianyip[num]; //染色体的变异概率
int bianyiflag[num];//染色体的变异情况
for(i=0;i<num;i++)//初始化
bianyiflag[i]=0;
//随机产生变异概率
srand((unsigned)time(NULL));
for(i=0;i<num;i++)
{
bianyip[i]=(rand()%100);
bianyip[i]/=100;
}
//确定可以变异的染色体
t=0;
for(i=0;i<num;i++)
{
if(bianyip[i]<pm)
{
bianyiflag[i]=1;
t++;
}
}
//变异操作,即交换染色体的两个节点
srand((unsigned)time(NULL));
for(i=0;i<num;i++)
{
if(bianyiflag[i]==1)
{
temp1=rand()%10;
temp2=rand()%10;
point=group[i].city[temp1];
group[i].city[temp1]=group[i].city[temp2];
group[i].city[temp2]=point;
}
}
}
int main()
{
int i,j,t;
init();
groupproduce();
//初始种群评价
pingjia();
t=0;
while(t++<MAXX)
{
xuanze();
//jiaopei();
bianyi();
pingjia();
}
//最终种群的评价
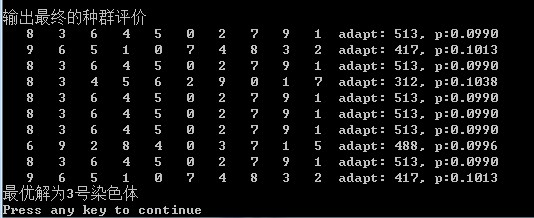
printf("\n输出最终的种群评价\n");
for(i=0;i<num;i++)
{
for(j=0;j<cities;j++)
{
printf("%4d",group[i].city[j]);
}
printf(" adapt:%4d, p:%.4f\n",group[i].adapt,group[i].p);
}
printf("最优解为%d号染色体\n",bestsolution);
return 0;
}