Dijkstra

迪杰斯特拉算法是典型的求解最短路径的方法。

优点，时间复杂度为O(n2)，主要思想就是遍历邻居，找到路径最短的邻居，添加到路径信息里面。再更新这个添加点，是否能减少到其他点的路径长度。

但是有一个缺点，就是这个算法只满足一个节点的扫描信息，如果想计算所有的节点到达其他节点的最短路径，就需要每次调用一次该算法。时间复杂度变为O(n3).

总体来说，分为两部分

第一部分：查找当前节点周围的最近的邻居；

min = INF;
        for(j=0;    j<MAXSIZE;  j++){
            if( !Final[j] && shotpathtable[j]<min){
                k = j;
                min = shotpathtable[j];
            }
        }

第二部分：超找通过这个最近的邻居，能否更快的到达其他的点。

for(j=0;    j<MAXSIZE;  j++){
            if( !Final[j] && (min + num[k][j]<shotpathtable[j])){
                shotpathtable[j] = min + num[k][j];
                path[j] = j;
            }
        }

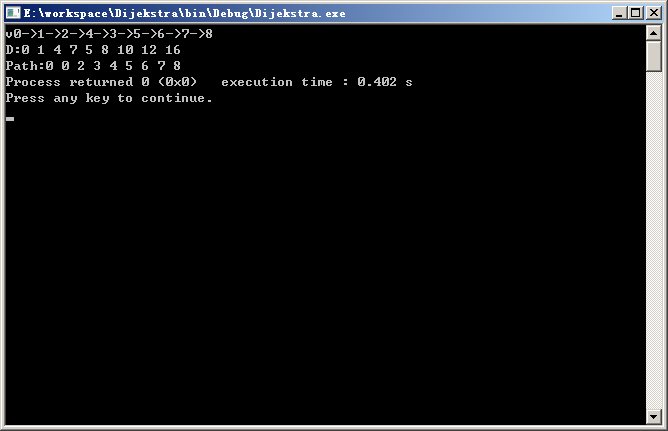
全部代码展示

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #define MAXSIZE 9
 4 #define INF 65535
 5 int num[MAXSIZE][MAXSIZE] = {
 6     0,    1,  5,INF,INF,INF,INF,INF,INF,
 7     1,    0,  3,  7,  5,INF,INF,INF,INF,
 8     5,    3,  0,INF,  1,  7,INF,INF,INF,
 9     INF,  7,INF,  0,  2,INF,  3,INF,INF,
10     INF,  5,  1,  2,  0,  3,  6,  9,INF,
11     INF,INF,  7,INF,  3,  0,INF,  5,INF,
12     INF,INF,INF,  3,  6,INF,  0,  2,  7,
13     INF,INF,INF,INF,  9,  5,  2,  0,  4,
14     INF,INF,INF,INF,INF,INF,  7,  4,  0
15 };
16 int main()
17 {
18     int path[MAXSIZE];
19     int shotpathtable[MAXSIZE];
20 
21     int v0 = 0;
22 
23     int i,j,v,w,k,min;
24     int Final[MAXSIZE];
25     for(i=0;    i<MAXSIZE;  i++){
26         Final[i] = 0;
27         shotpathtable[i] = num[v0][i];
28         path[i] = 0;
29     }
30     shotpathtable[v0] = 0;
31     Final[v0] = 1;
32     printf("v0");
33     for(i=1;    i<MAXSIZE;  i++){
34         min = INF;
35         for(j=0;    j<MAXSIZE;  j++){
36             if( !Final[j] && shotpathtable[j]<min){
37                 k = j;
38                 min = shotpathtable[j];
39             }
40         }
41         Final[k] = 1;
42         printf("->%d",k);
43         for(j=0;    j<MAXSIZE;  j++){
44             if( !Final[j] && (min + num[k][j]<shotpathtable[j])){
45                 shotpathtable[j] = min + num[k][j];
46                 path[j] = j;
47             }
48         }
49     }
50     printf("\n");
51     printf("D:");
52     for(i=0;    i<MAXSIZE;  i++){
53         printf("%d ",shotpathtable[i]);
54     }
55     printf("\nPath:");
56     for(i=0;    i<MAXSIZE;  i++){
57         printf("%d ",path[i]);
58     }
59     return 0;
60 }

运行结果