理解离散傅立叶变换(二)
理解离散傅立叶变换(二)
------实数形式离散傅立叶变换(Real DFT)
上一节我们看到了一个实数形式离散傅立叶变换的例子,通过这个例子能够让我们先对傅立叶变换有一个较 为形象的感性认识,现在就让我们来看看实数形式离散傅立叶变换的正向和逆向是怎么进行变换的。在此,我们先来看一下频率的多种表示方法。
一、
频域中关于频率的四 种表示方法
1、序 号表示方法,根据时域中信号的样本数取0 ~ N/2,用这种方法在程序中使用起来可以更直接地取得每种频率的幅度值,因为频率值跟数组的序号是一一对应的: X[k],取值范围是0 ~ N/2;
2、分 数表示方法,根据时域中信号的样本数的比例值取0 ~ 0.5: X[ƒ],ƒ = k/N,取值范围是0 ~ 1/2;
3、用 弧度值来表示,把
ƒ乘以一个2π得到一个弧度值,这种表示方法叫做自然频率(natural frequency):X[ω],ω = 2πƒ = 2πk/N,取值范围是0 ~ π;
4、以 赫兹(Hz)为单位来表示,这个一般是应用于一些特殊应用,如取样率为10 kHz表示每秒有10,000个样本数:取值范围是
0到取样率的 一半。
二、
DFT基本函数
ck[i] = cos(2πki/N)
sk[i] = sin(2πki/N)
其中k表示每个正余弦波的频率,如为2表示在0到N长度中存在两个完整的周期,10即有10个周期,如下图:
上图中至于每个波的振幅(amplitude)值(Re X[k],Im X[k])是怎么算出来的,这个是DFT的核心,也是最难理解的部分,我们先来看看如何把分解出来的正余弦波合成原始信号(Inverse DFT)。
三、
合成运算方法
(Real Inverse DFT)
DFT合成等式:

如果有学过傅立叶级数,对这个等式就会有似曾相识的感觉,不错!这个等 式跟傅立叶级数是非常相似的:

当然,差别是肯定是 存在的,因为这两个等式是在两个不同条件下运用的,至于怎么证明DFT合成公式,这个我想需要非常强的高等数学理论知识了,这是研究数学的人的工作,对于 普通应用者就不需要如此的追根究底了,但是傅立叶级数是好理解的,我们起码可以从傅立叶级数公式中看出DFT合成公式的合理性。
DFT合成等式中的Im
[k]和Re
[k]跟Im X[k]和Re X[k]是不一样的,下面是转换方法:

但k等于0和N/2时,实数 部分的计算要用下面的等式:

上面四个式中的N是时域中点 的总数,k是从0到N/2的序号。
为什么要这样进行转换呢?这 个可以从频谱密度(spectral density)得到理解,如下图就是个频谱图:

这是一个频谱图,横坐标表示 频率大小,纵坐标表示振幅大小,原始信号长度为N(这里是32),经DFT转换后得到的17个频率的频谱,频谱密度表示每单位带宽中为多大的振幅,那么带 宽是怎么计算出来的呢?看上图,除了头尾两个,其余点的所占的宽度是2/N,这个宽度便是每个点的带宽,头尾两个点的带宽是1/N,而Im X[k]和Re X[k]表示的是频谱密度,即每一个单位带宽的振幅大小,但Im
[k]和Re
[k]表 示2/N(或1/N)带宽的振幅大小,所以Im
[k]和Re
[k]分别应当是Im X[k]和Re X[k]的2/N(或1/N)。
频谱密度就象物理中物质密度, 原始信号中的每一个点就象是一个混合物,这个混合物是由不同密度的物质组成的,混合物中含有的每种物质的质量是一样的,除了最大和最小两个密度的物质外, 这样我们只要把每种物质的密度加起来就可以得到该混合物的密度了,又该混合物的质量是单位质量,所以得到的密度值跟该混合物的质量值是一样的。
至于为什么虚数部分是负数, 这是为了跟复数DFT保持一致,这个我们将在后面会知道这是数学计算上的需要(Im X[k]计算时加上了一个负号,Im
[k]再加上负号,结果便是正的,等于没有变化)。
如果已经得到了DFT结果, 这时要进行逆转换,即合成原始信号,则可按如下步骤进行转换:
1、先 根据上面四个式子计算得出Im
[k]和Re
[k]的值;
2、再 根据DFT合成等式得到原始信号数据。
下面是用BASIC语言来实现的转换源代码:
100 ‘DFT逆转换方法
110 ‘/XX[]数组存储计算结果(时域中的原始信号)
120 ‘/REX[]数组存储频域中的实数分量,IMX[]为虚分量
130 ‘
140 DIM XX[511]
150 DIM REX[256]
160 DIM IMX[256]
170 ‘
180 PI = 3.14159265
190 N% = 512
200 ‘
210 GOSUB XXXX ‘转到子函数去获取REX[]和IMX[]数据
220 ‘
230 ‘
240 ‘
250 FOR K% = 0 TO 256
260
REX[K%] = REX[K%] / (N%/2)
270
IMX[K%] = -IMX[K%] / (N%/2)
280 NEXT k%
290 ‘
300 REX[0] = REX[0] / N
310 REX[256] = REX[256] / N
320 ‘
330 ‘ 初始化XX[]数组
340 FOR I% = 0 TO 511
350
XX[I%] = 0
360 NEXT I%
370 ‘
380 ‘
390 ‘
400 ‘
410 ‘
420 FOR K% =0 TO 256
430
FOR I%=0 TO 511
440 ‘
450
XX[I%] = XX[I%] + REX[K%] * COS(2 * PI * K% * I% / N%)
460
XX[I%] = XX[I%] + IMX[K%] * SIN(2 * PI * K% * I% / N%)
470 ‘
480
NEXT I%
490 NEXT K%
500 ‘
510 END
上面代码中420至490换成如下形式也许更好理解,但结果都是一样 的:
420 FOR I% =0 TO 511
430
FOR K%=0 TO 256
440 ‘
450
XX[I%] = XX[I%] + REX[K%] * COS(2 * PI * K% * I% / N%)
460
XX[I%] = XX[I%] + IMX[K%] * SIN(2 * PI * K% * I% / N%)
470 ‘
480
NEXT I%
490 NEXT K%
四、
分解运算方法(
DFT
)
有三种完全不同的方法进行 DFT:一种方法是通过联立方程进行求解, 从代数的角度看,要从N个已知值求N个未知值,需要N个联立方程,且N个联立方程必须是线性独立的,但这是这种方法计算量非常的大且极其复杂,所以很少被 采用;第二种方法是利用信号的相关性(correlation)进行计算,这个是我们后面将要介绍的方法;第三种方法是快速傅立叶变换(FFT),这是一 个非常具有创造性和革命性的的方法,因为它大大提高了运算速度,使得傅立叶变换能够在计算机中被广泛应用,但这种算法是根据复数形式的傅立叶变换来实现 的,它把N个点的信号分解成长度为N的频域,这个跟我们现在所进行的实域DFT变换不一样,而且这种方法也较难理解,这里我们先不去理解,等先理解了复数 DFT后,再来看一下FFT。有一点很重要,那就是这三种方法所得的变换结果是一样的,经过实践证明,当频域长度为32时,利用相关性方法进行计算效率最 好,否则FFT算法效率较高。现在就让我们来看一下相关性算法。
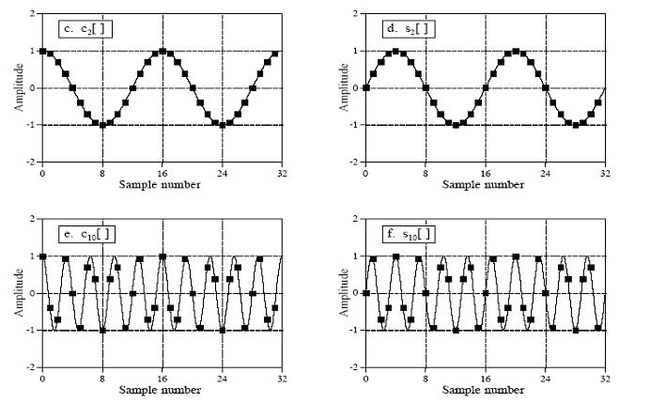
利用信号的相关性 (correlation)可以从噪声背景中检测出已知的信号,我们也可以利用这个方法检测信号波中是否含有某个频率的信号波:把一个待检测信号波乘以另 一个信号波,得到一个新的信号波,再把这个新的信号波所有的点进行相加,从相加的结果就可以判断出这两个信号的相似程度。如下图:

上面a和 b两个图是待检测信号波,图a很明显可以看出是个3个周期的正弦信号波,图b的信号波则看不出是否含有正弦或余弦信号,图c和d都是个3个周期的正弦信号 波,图e和f分别是a、b两图跟c、d两图相乘后的结果,图e所有点的平均值是0.5,说明信号a含有振幅为1的正弦信号c,但图f所有点的平均值是0, 则说明信号b不含有信号d。这个就是通过信号相关性来检测是否含有某个信号的方法。
相应地,我也可以通过把输入信号和每一种频率的正余弦信号进行相乘(关联操作),从而得到原始信号与 每种频率的关联程度(即总和大小),这个结果便是我们所要的傅立叶变换结果,下面两个等式便是我们所要的计算方法:

第二个式子中加了个负号,是为了保持复数形式的一致,前面我们知道在计算Im
[k]时又加了个负号,所以这只是个形式的问题,并没有实 际意义,你也可以把负号去掉,并在计算Im
[k]时 也不加负号。
这里有一点必须明白一个正交的概念:两个函数相乘,如果结果中的每个点的总和为0,则可认为这两个函 数为正交函数。要确保关联性算法是正确的,则必须使得跟原始信号相乘的信号的函数形式是正交的,我们知道所有的正弦或余弦函数是正交的,这一点我们可以通 过简单的高数知识就可以证明它,所以我们可以通过关联的方法把原始信号分离出正余弦信号。当然,其它的正交函数也是存在的,如:方波、三角波等形式的脉冲 信号,所以原始信号也可被分解成这些信号,但这只是说可以这样做,却是没有用的。
下面是实域傅立叶变换的BASIC语言代码:

到此为止,我们对傅立叶变换便有了感性的认识了吧。但要记住,这只是在实域上的离散傅立叶变换,其中 虽然也用到了复数的形式,但那只是个替代的形式,并无实际意义,现实中一般使用的是复数形式的离散傅立叶变换,且快速傅立叶变换是根据复数离散傅立叶变换 来设计算法的,在后面我们先来复习一下有关复数的内容,然后再在理解实域离散傅立叶变换的基础上来理解复数形式的离散傅立叶变换。