java实现树的一般操作

      树是数据结构中最基本的结构，今天的博客更新一下树的基本操作：

      树的节点结构：

      

package tree;


/**  
* TreeNode: 普通的树节点
* @author xuejupo  [email protected] 
* create in 2015-11-19 下午5:30:31  
*    
*/
public class TreeNode<T> {
	T value;
        
	TreeNode<T> leftChild;
	TreeNode<T> rightChild;

	TreeNode(T value) {
		this.value = value;
	}
	TreeNode() {
	}
	
	/**   增加左子节点
	* addLeft: 
	* @param value 
	* void  返回类型   
	*/
	public void addLeft(T value){
		TreeNode<T> leftChild = new TreeNode<T>(value);
		this.leftChild = leftChild;
	}
	/**  
	* addRight: 增加右子节点
	* @param value 
	* void  返回类型   
	*/
	public void addRight(T value){
		TreeNode<T> rightChild = new TreeNode<T>(value);
		this.rightChild = rightChild;
	}
	/* (non-Javadoc)
	 * @see java.lang.Object#equals(java.lang.Object)
	 * 重载equal方法
	 */
	@Override
	public boolean equals(Object obj) {
		// TODO Auto-generated method stub
		if(!(obj instanceof TreeNode)){
			return false;
		}
		return this.value.equals(((TreeNode<?>)obj).value);
	}
	/* (non-Javadoc)
	 * @see java.lang.Object#hashCode()
	 * 重载hashCode方法
	 */
	@Override
	public int hashCode() {
		// TODO Auto-generated method stub
		return this.value.hashCode();
	}
	@Override
	public String toString(){
		return this.value==null?"":this.value.toString();
	}
	
	
}

    树的基本操作类：

package tree;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

/**
 * TreeTools:树的操作类
 * 
 * @author xuejupo [email protected]
 * 
 *         create in 2015-11-19 下午5:31:05
 * 
 */
public class TreeTools {

	/**
	 * getTreeNum: 判断树中节点个数
	 * 
	 * @param root
	 *            根节点
	 * @return int 返回类型
	 */
	public static <T> int getTreeNum(TreeNode<T> root) {
		if (root == null) {
			return 0;
		}
		return getTreeNum(root.leftChild) + getTreeNum(root.rightChild) + 1;
	}

	/**
	 * getTreeDepth: 判断树的深度
	 * 
	 * @param root
	 *            根节点
	 * @return int 返回类型
	 */
	public static <T> int getTreeDepth(TreeNode<T> root) {
		if (root == null) {
			return 0;
		}
		int leftDepth = getTreeDepth(root.leftChild) + 1;
		int rightDepth = getTreeDepth(root.rightChild) + 1;
		return Math.max(leftDepth, rightDepth);
	}

	/**
	 * preOrderTravel: 前序遍历
	 * 
	 * @param root
	 *            void 返回类型
	 */
	public static <T> void preOrderTravel(TreeNode<T> root) {
		if (root == null) {
			return;
		}
		visitNode(root);
		preOrderTravel(root.leftChild);
		preOrderTravel(root.rightChild);
	}

	/**
	 * midOrderTravel: 中序遍历
	 * 
	 * @param root
	 *            void 返回类型
	 */
	public static <T> void midOrderTravel(TreeNode<T> root) {
		if (root == null) {
			return;
		}
		midOrderTravel(root.leftChild);
		visitNode(root);
		midOrderTravel(root.rightChild);
	}

	/**
	 * backOrderTravel: 后序遍历
	 * 
	 * @param root
	 *            void 返回类型
	 */
	public static <T> void backOrderTravel(TreeNode<T> root) {
		if (root == null) {
			return;
		}
		backOrderTravel(root.leftChild);
		backOrderTravel(root.rightChild);
		visitNode(root);
	}

	/**
	 * visitNode: 访问node节点
	 * 
	 * @param node
	 *            void 返回类型
	 */
	private static <T> void visitNode(TreeNode<T> node) {
		System.out.print(node.value + "\t");
	}

	/**
	 * levelTravel: 分层遍历
	 * 
	 * @param root
	 *            void 返回类型
	 */
	public static <T> void levelTravel(TreeNode<T> root) {
		Queue<TreeNode<T>> q = new LinkedList<TreeNode<T>>();
		q.offer(root);
		while (!q.isEmpty()) {
			TreeNode<T> temp = q.poll();
			visitNode(temp);
			if (temp.leftChild != null) {
				q.offer(temp.leftChild);
			}
			if (temp.rightChild != null) {
				q.offer(temp.rightChild);
			}
		}
	}

	/**
	 * getNumForKlevel: 求第K层节点个数
	 * 
	 * @param root
	 * @param k
	 * @return int 返回类型
	 */
	public static <T> int getNumForKlevel(TreeNode<T> root, int k) {
		if (root == null || k < 1) {
			return 0;
		}
		if (k == 1) {
			return 1;
		}
		int leftNum = getNumForKlevel(root.leftChild, k - 1);
		int rightNum = getNumForKlevel(root.rightChild, k - 1);
		return leftNum + rightNum;
	}

	/**
	 * getLeafNum: 求二叉树中叶子节点的个数
	 * 
	 * @param root
	 * @return int 返回类型
	 */
	public static <T> int getLeafNum(TreeNode<T> root) {
		if (root == null) {
			return 0;
		}
		if (root.leftChild == null && root.rightChild == null) {
			return 1;
		}
		int leftNum = getLeafNum(root.leftChild);
		int rightNum = getLeafNum(root.rightChild);
		return leftNum + rightNum;
	}

	/**
	 * exchange: 交换根节点的左右子树
	 * 
	 * @param root
	 * @return TreeNode 返回类型
	 */
	public static <T> TreeNode<T> exchange(TreeNode<T> root) {
		if (root == null) {
			return null;
		}
		TreeNode<T> left = exchange(root.leftChild);
		TreeNode<T> right = exchange(root.rightChild);
		root.leftChild = right;
		root.rightChild = left;
		return root;
	}

	/**
	 * nodeIsChild: 查看node是否是root的子节点
	 * 
	 * @param root
	 * @param node
	 * @return boolean 返回类型
	 */
	public static <T> boolean nodeIsChild(TreeNode<T> root, TreeNode<T> node) {
		if (root == null || node == null) {
			return false;
		}
		if (root == node) {
			return true;
		}
		boolean isFind = nodeIsChild(root.leftChild, node);
		if (!isFind) {
			isFind = nodeIsChild(root.rightChild, node);
		}
		return isFind;
	}

	/**
	 * findAllFatherNode: 返回两个节点lnode和rnode的以root为根节点的公共父节点
	 * 
	 * @param root
	 *            根节点
	 * @param lNode
	 * @param rNode
	 * @return TreeNode 返回类型
	 */
	public static <T> TreeNode<T> findAllFatherNode(TreeNode<T> root,
			TreeNode<T> lNode, TreeNode<T> rNode) {
		if (lNode == root || rNode == root) {
			return root;
		}
		if (root == null || lNode == null || rNode == null) {
			return null;
		}
		// 如果lNode是左子树的节点
		if (nodeIsChild(root.leftChild, lNode)) {
			if (nodeIsChild(root.rightChild, rNode)) {
				return root;
			} else {
				return findAllFatherNode(root.leftChild, lNode, rNode);
			}
		} else {
			if (nodeIsChild(root.leftChild, rNode)) {
				return root;
			} else {
				return findAllFatherNode(root.rightChild, lNode, rNode);
			}
		}
	}

	/**
	 * getTreeFromPreAndMid: 根据前序和中序构建二叉树
	 * 
	 * @param pre
	 *            前序序列
	 * @param mid
	 *            中序序列
	 * @return TreeNode 返回类型
	 */
	public static <T> TreeNode<T> getTreeFromPreAndMid(List<T> pre, List<T> mid) {
		if (pre == null || mid == null || pre.size() == 0 || mid.size() == 0) {
			return null;
		}
		if (pre.size() == 1) {
			return new TreeNode<T>(pre.get(0));
		}
		TreeNode<T> root = new TreeNode<T>(pre.get(0));
		// 找出根节点在中序中的位置
		int index = 0;
		while (!mid.get(index++).equals(pre.get(0))) {
		}
		// 构建左子树的前序
		List<T> preLeft = new ArrayList<T>(index);
		// 左子树的中序
		List<T> midLeft = new ArrayList<T>(index);
		for (int i = 1; i < index; i++) {
			preLeft.add(pre.get(i));
		}
		for (int i = 0; i < index - 1; i++) {
			midLeft.add(mid.get(i));
		}

		// 重建左子树
		root.leftChild = getTreeFromPreAndMid(preLeft, midLeft);
		// 右子树的前序
		List<T> preRight = new ArrayList<T>(pre.size() - index - 1);
		// 右子树的中序
		List<T> midRight = new ArrayList<T>(pre.size() - index - 1);
		for (int i = 0; i <= pre.size() - index - 1; i++) {
			preRight.add(pre.get(index + i));
		}
		for (int i = 0; i <= pre.size() - index - 1; i++) {
			midRight.add(mid.get(index + i));
		}
		// 重建→子树
		root.rightChild = getTreeFromPreAndMid(preRight, midRight);
		return root;
	}

	/**
	 * equals: 查看node1和node2两棵树是否相等(两棵树所有节点都相等)
	 * 
	 * @param node1
	 *            node2 两个节点
	 * @return boolean 返回类型
	 */
	public static <T> boolean equals(TreeNode<T> node1, TreeNode<T> node2) {
		// TODO Auto-generated method stub
		if (node1 == null && node2 == null) {
			return true;
		} else if (node1 == null || node2 == null) {
			return false;
		}
		boolean isEqual = node1.value.equals(node2.value);
		boolean isLeftEqual = equals(node1.leftChild, node2.leftChild);
		boolean isRightEqual = equals(node1.rightChild, node2.rightChild);
		return isEqual && isLeftEqual && isRightEqual;
	}
}

   测试类：

     测试类中，先利用节点中的基本操作构建一棵树：

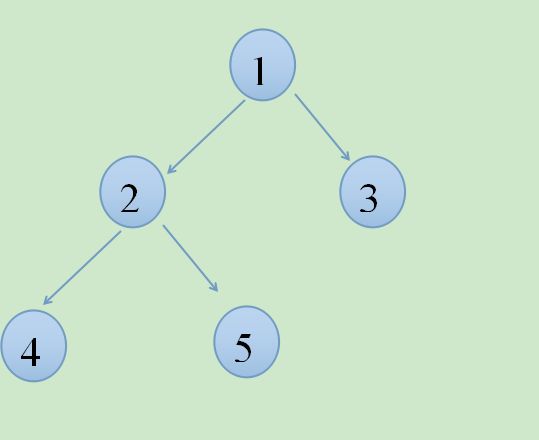
   图1         简单树
 

      然后测试了操作类里面几个基本的操作，包括前序和后序遍历，然后根据树的前序序列和中序序列，初始化两个list，分别作为要构建的新树的前序和中序去构建一棵新树，然后比较两棵树是否相同。

     代码：

public static void main(String[] args) {
		// TODO Auto-generated method stub
		TreeNode<Integer> t = new TreeNode<Integer>(1);
		t.addLeft(2);
		t.addRight(3);
		t.leftChild.addLeft(4);
		t.leftChild.addRight(5);
		System.out.println("中序遍历测试:");
		TreeTools.midOrderTravel(t);
		System.out.println("\n前序遍历测试:");
		TreeTools.preOrderTravel(t);
		System.out.println("\n后序遍历测试:");
		TreeTools.backOrderTravel(t);
		System.out.println("\n层次遍历测试:");
		TreeTools.levelTravel(t);
		System.out.println("\n树的深度:"+TreeTools.getTreeDepth(t));
		System.out.println("树的叶子个数:"+TreeTools.getLeafNum(t));
		System.out.println("树的节点个数:"+TreeTools.getTreeNum(t));
		System.out.println("第2层节点个数为:"+TreeTools.getNumForKlevel(t,2));
		List<Integer> pre = new ArrayList<Integer>();
		pre.add(1);
		pre.add(2);
		pre.add(4);
		pre.add(5);
		pre.add(3);
		List<Integer> mid = new ArrayList<Integer>();
		mid.add(4);
		mid.add(2);
		mid.add(5);
		mid.add(1);
		mid.add(3);
		TreeNode<Integer> root = TreeTools.getTreeFromPreAndMid(pre, mid);
		System.out.println("\n通过前序和中序构建树测试：");
		TreeTools.levelTravel(root);
		System.out.println("\n构建的树比较测试:");
		System.out.println(TreeTools.equals(t,root));
	}

 结果为：

中序遍历测试:
4	2	5	1	3	
前序遍历测试:
1	2	4	5	3	
后序遍历测试:
4	5	2	3	1	
层次遍历测试:
1	2	3	4	5	
树的深度:3
树的叶子个数:3
树的节点个数:5
第2层节点个数为:2

通过前序和中序构建树测试：
1	2	3	4	5	
构建的树比较测试:
true

     最后的话：  树的基本操作都很简单，树是我见过的最适合用递归来操作的数据结构了。因为子节点和父节点是一样的类型，而且基本具有同样的属性。

        以上的方法里面，可能只有利用前序和中序构建一棵树不容易理解。   比如图1里面那棵树，前序是1 2 4 5 3   中序是4 2 5 1 3   前序的1表示根是1，然后在中序序列里，1左边的是根节点的左子树，1后边的是整棵树的右子树，中序1前边有3个数字，右边有1个数字，表示根节点的左子树有3个节点，右子树有1个节点，所以构建根节点左子树的前序和中序时，取根节点前序的2，4，5和根节点中序的425，构建根节点右子树的前序和中序时取根节点的3，然后递归构建即可。