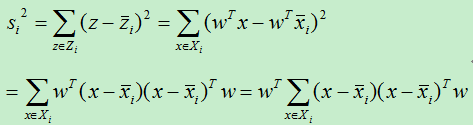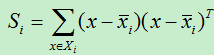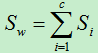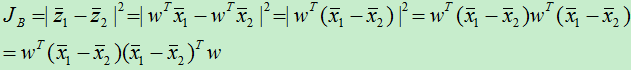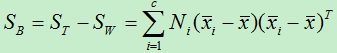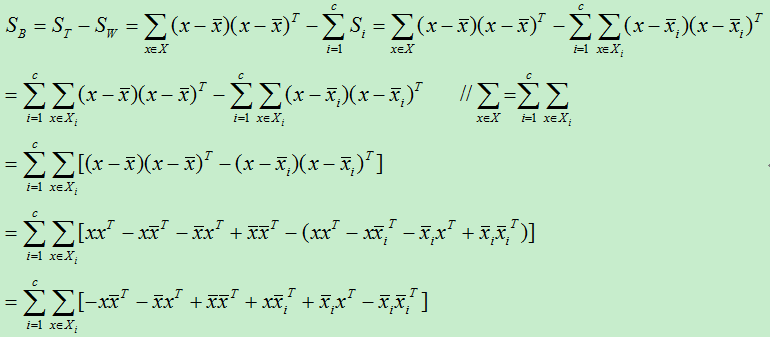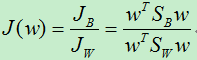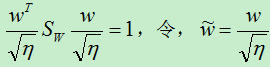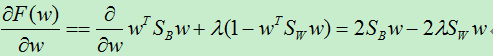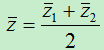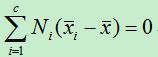LDA 线性判别分析
LDA, Linear Discriminant Analysis，线性判别分析。注意与LDA（Latent Dirichlet Allocation，主题生成模型）的区别。
1、引入
上文介绍的PCA方法对提取样本数据的主要变化信息非常有效，而忽略了次要变化的信息。在有些情况下，次要信息可能正是把不同类别区分开来的分布方向。简单来说，PCA方法寻找的是数据变化的主轴方向，而判别分析寻找的是用来有效分类的方向。二者侧重点不同。在图1.1可以看出变化最大的方向不一定能最好的区分不同类别。
图1.1 用PCA和LDA对数据进行投影
2、LDA算法分析
LDA算法主要用来对样本进行分类，其分类的核心思想是：将高维样本数据投影到最佳分类的向量空间，保证在新的子空间中，有更大的类间距离和更小的类内距离。
设样本数据为：
，将原始样本经过w变换后变成了z，其中
，变换规则为：
变换的目的在于使得同一类的样本被w作用后距离更近，不同类的样本被w作用后距离更远。为了能更好的度量类内距离和类间距离，我们先定义中心点，即均值，设Xi为类别ci的样本数据的集合，则Xi的中心点为：
Ni为类别ci的样本数，即Xi的数目。
此中心点经过w变换后得到的中心点为：
即样本集Xi的中心点的投影为Xi中各元素投影后的均值。
现在，我们需要使得投影之后同类之间样本距离更小，而不同类之间的样本距离越大。为此，我们通过定义类间距离和类内距离：
1）类内距离。
类内距离主要用各样本点到该样本点所在类别的中心点的距离和来表示。我们使用散列度来表示一个类别的类内距离。对于投影之后类别为i的类内散列度(scatter，类似方差)为：
其中Zi表示类别为i的所有样本集合。将上式进行变换得：
为了使得表达式简介，令：
所以有：
上式只是一个类别的散列度，若将所有类别的散列度相加，便得到整个样本的类内离散度：
将上式进行整理：
令：
所以：
其中，Sw被称为类内散度矩阵。
2）类间距离。
类间距离主要通过两个类之间的中心点距离来衡量。但是当类别很多时如何计算类间距离呢？下面分别进行分析。
A）只有两个类别时。假设两个类别样本数据分别为z1,z2，此时，类间离散度为：
其中，
将上式整理成只包含x的式子：
令：
于是：
其中，SB被称为类间散度矩阵。
B）有多个类别时。根据只有两个类别的情况，我们很容易可以得到类间离散度为：
此时共有c(c-1)/2项的求和，时间复杂度为O(c2)。
通过上式，我们可以求得相应的类间散度矩阵为：
可能是这种方法复杂度太高，故而LDA并没有使用这种方法来计算多类别的类间离散度，而是采用了一种比较间接的方式。首先定义X的整体散度矩阵，
样本集的整体散度为类间散度和类内散度之和：
于是类间散度可是使用下式来进行计算：
现在我们对上式进行推导：
为了更加清楚的求解上式，我们将里面的求和搬出来进行分析：
将上式代入上上式得：
同样，最终得到类间散度为：
SB：为类间散度矩阵。
至此，我们已经得到了类内散度JW和类间散度JB，现在可以使用这两个散度来构造目标函数J(w)：
现在，我们需要求得目标函数最大时的w，因为这时通过w映射后的样本数据具有最佳的类间距离和类内距离。从目标函数可以看出。当w成倍的放大或缩小时，目标函数保持不变，因而我们通过目标函数最大只能得到w的方向。为了使得计算简单，我们假设分母的值为1，即：
首先，上式的计算结果是一个数，而不是一个向量或矩阵，于是我们可以设为：
即：
于是有：
因为我们最终求得的w的大小是可以随意的，只是方向是确定的，因此，我们将上面的分母设为1是合理的。
这时我们将原问题转化成了有约束的最优化问题：
看到此问题毫不犹豫的想起了用了无数次的拉格朗日定理，于是，我们使用拉格朗日乘子得：
对w求导：
令导数为零：
上式中的Sw若可逆则可以直接移到等式左边，但是当样本维数较高，而样本数较少时，这时的Sw可能为奇异矩阵。此时可以考虑先使用PCA对样本进行降维，然后再对降维后的数据使用LDA。
在此，先假设Sw是可逆的，则有：
这就是传说中的Fisher Linear Discriminantion公式。其实FLD和LDA在很多情况下可以互换。
现在，我们可以看出w为上面式子的特征向量，而我们需要的w为特征值最大时所对应的特征向量。特征值最大，意味着在对应的特征向量上的变化最大。
上式的
不一定是对称矩阵，在求它的特征向量时不能使用奇异值分解，这样就只能使用普通的求特征向量的方式，普通的方式时间复杂度为O(n3)，
于是我们对上式中的SBw进行分析得到：
于是：
至此，我们已经得到了样本的最佳映射w，w=(w1,w2,…,wd’)，当我们将样本集x使用w进行映射后得到了具有最佳分类效果的样本z。
3、LDA分类
那么在最佳的分类空间如何对样本进行分类？
1）对二分类问题。由于只有两个类别，在经过上面的求解后，最后所有样本将会映射到一维空间中，设两个不同样本映射后的中心点分别为
，我们将两个类别的中心点之间中心点作为分类点。
最后，我们将
的x分为一类，其他的分为另一类。
2）对多分类问题。通过LDA方法最终将原始数据映射到c-1个维度上，现在我们需要在这c-1个维度上将样本集分成c类。这个怎么分呢？本人暂时也不知道，能想到的只是将问题转化为二分类问题。实际上，对于多类的情况主要考虑用来降维。
对于此类问题，我们主要将它转化为二分类来处理，我们使用一对其余的方法。简单来说就是先将所有c类样本分成1和2~c，然后再将2~c分为2和3~c，以此类推，直到完全分开。
3、维度分析和总结
上面我们将原样本的维度从d维降到了d’(此时使用d’来表示
，d’<d)。那么d’到底最大是多少呢？因为特征向量是通过
而求出，所以特征向量的维数d’不会大于的秩。而SB的秩
而：
存在线性组合使得：
所以有：
因此：
所以通过LDA算法进行映射的最终空间维度不会超过c-1个维度。当只有两个类别时，那么就只能将其投影到一维的空间中进行分类。
在我们进行多分类时，并不是真的直接在c-1个维度上将样本分成c类，而是拆分成二分类的情况来进行分类。而我们千辛万苦推导出来的多分类的情形主要用来降维。
另外，本人认为应该可以在c-1个维度上对c个类别的样本进行划分，只是本人尚未发现好的方法！
在实际应用中，LDA算法表现出来的效果相比其他方法并不十分理想（一般情况下）。并且还可能会出现过拟合的情况。但是LDA算法的这种数学思想非常值得学习研究！
参考文献：
[1] Richard O. Duda, 模式分类
[2] peghoty, http://blog.csdn.net/itplus/article/details/12038357
http://blog.csdn.net/itplus/article/details/12038441
[3] http://www.cnblogs.com/cfantaisie/archive/2011/03/25/1995849.html