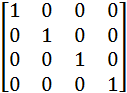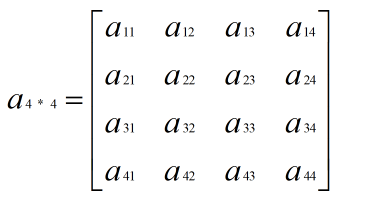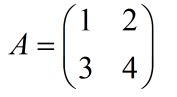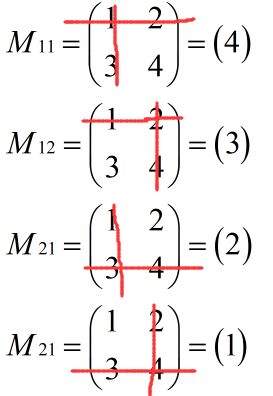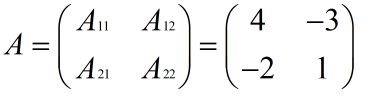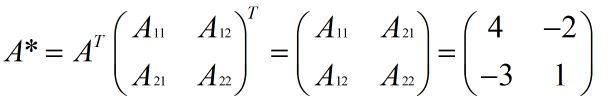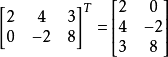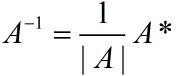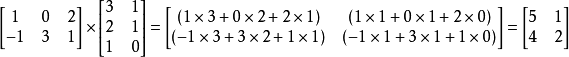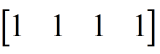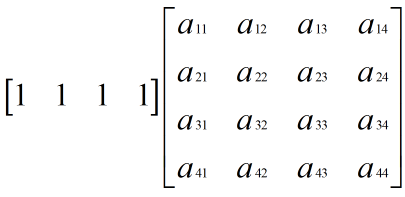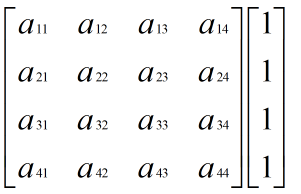Matrix 矩阵
单位矩阵
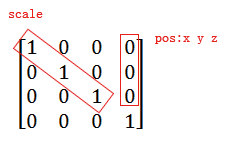
4X4单位矩阵E:
4*4矩阵表示4行4列:
伴随矩阵
求解方法:
1. 把矩阵的各个元素换成它的代数余子式;
2. 将所得到的矩阵转置便得到A的伴随矩阵;
代数余子式:在一个n阶行列式中,把元素aij (i,j=1,2,.....n)所在的行与列划去后,剩下的(n-1)^2个元素按照原来的次序组成的一个n-1阶行列式Mij,称为元素aij的余子式,Mij带上符号(-1)^(i+j)称为aij的代数余子式,记作Aij=(-1)^(i+j) Mij。
例:
解:A11 = (-1)^(1+1)*M11 = (-1)^(1+1)*4 = 4;
A12 = (-1)^(1+2)*M11 = (-1)^(1+2)*3 = -3;
A21 = (-1)^(2+1)*M11 = (-1)^(2+1)*2 = -2;
A22 = (-1)^(2+2)*M11 = (-1)^(2+2)*1 = 1;
所以
转置矩阵
把矩阵A的行换成同序数的列所得到的新矩阵称为A的转置矩阵,这一过程称为矩阵的转置。
逆矩阵
设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E。 则我们称B是A的逆矩阵,而A则被称为可逆矩阵。
矩阵的乘法:两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵
测试Unity 矩阵:
得出结果:
从输出可以看到unity的矩阵采用矩阵左乘法,即向量用列向量表示, 也正是因为采用列向量表示, 矩阵的16个元素(m[i]:i表示0~15)前面是个是第一列,然后是第二列,第三列和第四列。
Row 行;Cloum 列。
行矩阵:只有一行的矩阵,一般在矩阵中采用右乘。
列矩阵:只有一列的矩阵,一般在矩阵中采用左乘,
Unity Shader
在Vertex Function函数中,将模型空间的顶点转换到投影空间, o.pos = mul(UNITY_MATRIX_MVP, v.vertex); 理解为矩阵采用左乘,顶点向量是列向量,使用齐次坐标得到4X1的矩阵.
将法向量转到世界空间
顶点从模型空间转换到世界坐标空间只需要乘以世界转换矩阵即可,但是顶点的法向量却不能通过直接乘以这个矩阵将其变换到世界空间。原因是世界矩阵不仅包含旋转,还有可能包含着缩放操作,如果模型被不成比例的缩放,在不同方向上会有不同程度的拉伸或者压缩,顶点的坐标会因而伸缩,但是如果对法向量进行同样的伸缩,那么变化后的法向量将不再垂直于对应的表面。因此对应没有缩放或等比缩放的世界转换矩阵,可以直接采用相同的转换矩阵作为法向量的变换矩阵。
对于法向量来讲,只有方向,对于平移不起任何作用,如果我们采用_Object2World,那么它的旋转和缩放都进行了变换,我们不想让它的缩放进行变换。我们就要构造新的矩阵M,屏蔽掉它的缩放,但是保留它的旋转。现在将_Object2World的逆矩阵_World2Object转置就得到M矩阵了。
float3 normalDirection = normalize( mul(float4(v.normal,0.0),_World2Object)).xyz; 本来应该是mul((float4(v.normal,1.0),_World2Object的转置);
关于转置,可以变换矩阵和向量相乘的顺序,这样就相当于和转置矩阵相乘了。
二维旋转矩阵
在二维空间中,旋转可以用一个单一的角 θ 定义。作为约定,正角表示逆时针旋转。把笛卡尔坐标的列向量关于原点逆时针旋转θ 的矩阵是:
顺时针旋转就之间计算-θ 即可。
逆矩阵:
逆矩阵表示较原来反方向旋转θ ,也即顺时针旋转-θ;