数据结构与算法：算法分析

目录 

实验研究
常用函数
渐近分析 

一.实验研究（Experimental studies）

1.运行时间测量

• 时钟时间 time.time()
• CPU时间 time.clock()
• 基准时间 timeit.timeit()

在执行算法的时候，我们可以通过改变输入规模的大小和记录花费的时间来研究运行时间。

在python中使用time模块的time函数来记录算法的运行时间：

from time import time
start_time=time()
run algorithm
end_time=time()
elapsed=end_time-start_time #运行时间

 

由于许多进程使用计算机的CPU，所以在测试时，运行时间也将取决于在计算机上运行的其他进程。所以一个更公平

的衡量标准是计算CPU cycles，会使用到time.clock()函数。但是即使使用这种方法，在同一电脑上执行同一算法，

测试结果也可能不同，它取决于电脑的系统，所以在python中更好的方法是使用timeit模块。

 2.实验研究中的挑战/困难

• 实验中两个算法的运行时间很难直接进行比较除非实验在相同的硬件和软件环境中执行
• 实验中只能完成有限的输入规模，所以一些重要的输入可能会被遗漏掉
• 一个算法必须完全执行才能研究它的实验运行时间（实验研究中最严重的缺点）

3.超越实验分析

为了分析算法的运行时间而不执行实验，我们直接对一个算法的高级描述（可以是一个实际的代码片段或者是

语言无关的伪代码（pseudo-code））进行分析。我们定义一系列的基本操作：

• Assigning an identifier to an object
• Determining the object associated with an identifier
• Performing an arithmetic operation (for example, adding two numbers)
• Comparing two numbers
• Accessing a single element of a Python list by index
• Calling a function (excluding operations executed within the function)
• Returning from a function

不去确定每个基本操作的具体时间,我们只需记录每个基本操作的执行次数,并使用 t 来衡量算法的执行时间。

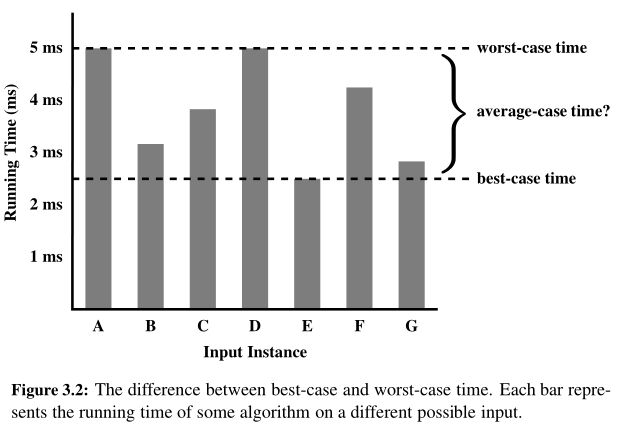
4.最坏情况分析和最好情况分析

最坏情况分析比平均情况分析容易的多，它只需要识别最坏情况的输入，对我们来说比较简单。

二.常用函数

1.The Constant Function-常数函数

　　f(n)=c

2.The Logarithm Function-对数函数

　　f(n)=log_bn ,n>1

通常情况下，会忽略掉基数：logn=log₂n

性质：对于任何实数a>0,b>1,c>0,d>1,

 3.The Linear Function-线性函数

　　f(n)=n

 4.The N-Log-N Function

　　f(n)=nlogn

 5.The Quadratic Function-二次函数

　　f(n)=n²

 6.The Cubic Function and Other Polynomials-立方函数和其他多项式

　　立方函数：f(n)=n³

　　多项式：

 7.The Exponential Function-指数函数

　　f(n)=bⁿ

三.渐近分析

1.渐近记号

01--大O记号

定义--O(g(n))={f(n):存在正常数c和n₀,使对所有的n≥n₀,有0≤f(n)≤c*g(n)}

理解--O(g(n))是一个函数集合，f(n)是满足条件的一个函数，。

大O记号在一个常数因子内给出一个函数的上界。

02--大Ω记号

定义--Ω(g(n))={f(n):存在正常数c和n₀,使对所有的n≥n₀,有0≤c*g(n)≤f(n)}

理解--在这里，大Ω记号给出了一个函数的下界。

03--大Θ记号

定义--Θ(g(n))={f(n):存在正常数c₁，c₂和n₀,使对所有的n≥n₀,有0≤c₁*g(n)≤f(n)≤c₂*g(n)}

理解--对于任一函数f(n),若存在正常数c₁，c_{2,当n充分大时，f(n)能被夹在c1*g(n)和c2*g(n)之间}

如图所示，三种记号的图例：

2.举例分析

01--Analysis of the Maximum-Finding Algorithm

查找最大值代码如下

def find_max(data):
    biggest = data[0]
    for val in data:
        if val > biggest ：
            biggest = val 
    return biggest 

 

分析--我们在这里分析的是biggest别赋值的次数：

最坏情况下，data如果以递增顺序排列，biggest需要被赋值n-1次,该赋值语句运行时间为O(n)

但是如果data是随机的排列的。在循环中，只有当val>biggest的时候，biggest才会被赋值。如果序列是随机的顺序，

循环到第j个元素时，第j个元素是前j个元素中最大值得概率为1/j，所以biggest被赋值的次数=1+1/2+1/3...+1/n.

即。

根据下面这个定理，可以得知biggest赋值语句运行时间为O(logn)

02--Three-Way Set Disjointness

有3个序列A，B，C，假设每个序列里面没有重复的元素，但是三个序列中会有相同的元素。

disjoint1函数用来判断三个序列中是否含有元素x既存在A中，又存在B中还有C中。

 

def disjoint1(A,B,C):
    for a in A:
        for b in B:
            for c in C:
                if a==b==c:
                    return False
    return True

 

分析--从代码中很容易看出----最坏情况下，该算法的运行时间为O(n³)

加强版：disjoint2函数如下

def disjoint2(A,B,C):
    for a in A:
        for b in B:
            if a==b:
                for c in C:
                    if a==c:
                        return False
    return True

 

分析--最坏情况下，该算法的运行时间为O(n²)。最坏情况下，A中的每个元素都和B中的都一样，

则C中的循环执行n次，所以A和C中循环运行时间为O(n)，B中循环运行时间为O(n²).所以最坏

情况下，该算法的运行时间为O(n²)。

03--Element Uniqueness

和上个例子相关的问题就是集合中每个元素是独一无二的问题。

第一种解决方法是使用嵌套循环，外层index为j，内层index为k，k从j+1开始遍历数组。代码如下：

def unique1(S):
    for j in range(len(S)):
        for k in range(j+1,len(s)):
            if S[j]==S[k]:
                return False
    return True

 

 分析--第一次执行外层循环时，内层循环执行n-1次，第二次执行外层循环时，内层循环执行n-2次，

所以最坏情况下，内层循环共执行(n-1)+(n-2)+...+2+1=n(n-1)/2,运行时间为O(n²)

第二种解决方法是先将序列进行排序，再进行比较，代码如下：

def unique2(S):
    temp=sorted(S)
    for j in range(1,len(S)):
        if S[j-1]==S[j]:
            return False
    return True

 

分析--代码中使用python内置函数sorted()对序列进行排序，排序算法保证了最坏运行时间为O(nlogn)。

排序完成后，循环序列运行时间为O(n)。所以该算法最坏运行时间为O(nlogn)

 

 Data Structures and Algorithmin Python讲的很细。

初步的算法分析算是看完了，进度这么慢，只能假期来凑喽

注：转载请注明出处