【线性代数公开课MIT Linear Algebra】 第一课 矩阵的行图像与列图像
本系列笔记为方便日后自己查阅而写,更多的是个人见解,也算一种学习的复习与总结,望善始善终吧~
1. 从方程组到矩阵
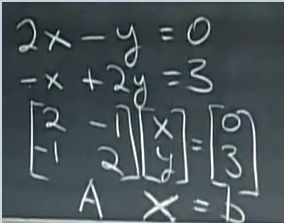
矩阵的诞生是为了用一种简洁的方式表达线性方程组
个人理解来说就是为了更好的描述和解决 Ax = b
从系统的角度来理解:
A 就是我们的系统
x 就是我们的输入
b 就是我们的输出
2. row picture 行图像
矩阵分为行row和列column
顾名思义,row picture关注矩阵的行部分
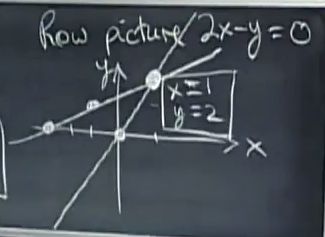
将行所代表的方程以直线形式画出即可得到行图像
(童鞋们应该非常熟悉,从小到大学校教导的就是这一思维)
3. column picture 列图像
column picture关注列的部分,而一列即一个向量vector
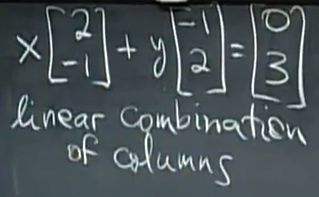
现在问题转化为了找到一个合适的linear combination(线性组合)使得Ax = b
对应的图
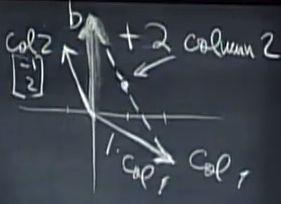
vector b 即为两个col vector之和
这里又引申出当vector x任取时,我们可以获得整个xy平面,意味着无论vector b是什么都能找到对应解
(当两个col vector 平行时则不行)
* column picture的做法感觉在学校不怎么强调,但这种理解方式更有助于掌握矩阵和向量
接下来老师就把2D延伸到了3D
做法与结论都一样,那么当超过3D之后我们很难直观的描述,这时矩阵的优势便得以体现
就这样一步一步我们抽象出了Ax = b 的本质
现在我们拥有了矩阵这一概念,下面要做的便是探究其属性和寻找合适的算法用于解决问题
PS:本文图片皆来自公开课视频截图