Chapter 4 | Trees and Graphs--检查一棵树是否平衡以及判断一棵树是否为平衡二叉树

4.1  Implement a function to check if a tree is balanced. For the purposes of this question, a balanced tree is defined to be a tree such that no two leaf nodes differ in distance from the root by more than one.

译文：实现一个函数检查一棵树是否平衡，对于这个问题而言，平衡是指这棵树任意两个叶子节点到根节点的距离相差不超过 1。

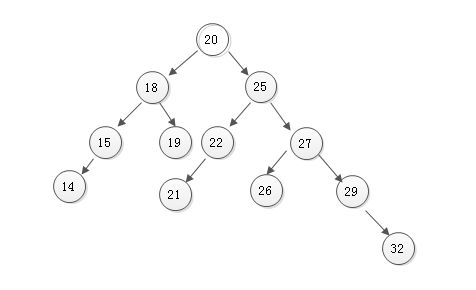
需要注意的是这里不是判断一棵树是否为平衡二叉树，一棵树为平衡二叉树，不一定满足这个问题中的平衡，但是满足这个平衡条件的二叉查找树就一定是平衡二叉树。

就上面这棵二叉树而言，它是平衡二叉树，但并不满足问题中的平衡条件。

方法一：直接计算树的最大高度和最小高度

即计算根节点到所有叶子节点的距离的最大值和最小值，直接通过递归计算

/*最大高度*/
int AvlTree::MaxDepth(AvlNode *node)
{
	int left, right;
	if (NULL == node)
		return -1;

	left = MaxDepth(node->leftchild);
	right = MaxDepth(node->rightchild);

	return (left > right) ? (left + 1) : (right + 1);
}
/*最小高度*/
int AvlTree::MinDepth(AvlNode *node)
{
	int left, right;
	if (NULL == node)
		return -1;

	left = MinDepth(node->leftchild);
	right = MinDepth(node->rightchild);
	
	return (left < right) ? (left + 1) : (right + 1);
}

判断平衡，则只需判断最大高度与最小高度的差值是否小于1

bool AvlTree::isBalanced(void)
{
	/*cout << MaxDepth(Root) << endl;
	cout << MinDepth(Root) << endl;*/
	return (MaxDepth(Root) - MinDepth(Root) <= 1);
}

其余部分代码见 http://blog.csdn.net/wenqian1991/article/details/21889147。

测试代码：

int main()
{
	AvlTree avltree;
	avltree.Insert(20);
	avltree.Insert(18);
	avltree.Insert(25);
	avltree.Insert(15);
	avltree.Insert(19);
	avltree.Insert(22);
	avltree.Insert(27);
	avltree.Insert(14);
	avltree.Insert(21);
	avltree.Insert(26);
	avltree.Insert(29);
	avltree.Insert(32);

	if (avltree.isBalanced())
		cout << "yes" << endl;
	else
		cout << "no" << endl;

	return 0;
}

方法二、计算每个叶子节点的深度

这里我们判断的参考对象均为二叉树（AVL），计算每个叶子节点的深度，这里我们采用中序遍历的方式，记录下所有叶子节点的深度。

void AvlTree::GetDepth(AvlNode *node, int *Arr, int *Num, int Depth)
{
	if (NULL == node)
		return;
	++Depth;
	GetDepth(node->leftchild, Arr, Num, Depth);
	if (NULL == node->leftchild && NULL == node->rightchild)
		Arr[(*Num)++] = Depth;
	GetDepth(node->rightchild, Arr, Num, Depth);
	--Depth;  //递归每次回转时，高度减1
}

bool AvlTree::isBalanced(void)
{
	int Arr[100];
	int Num = 0, Depth = -1;
	GetDepth(Root, Arr, &Num, Depth);

	int max = Arr[0], min = Arr[0];
	for (int i = 1; i < Num; ++i)
	{
		if (Arr[i] > max) max = Arr[i];
		if (Arr[i] < min) min = Arr[i];
	}

	return (max - min <= 1);
}

这里再额外补充判断一棵二叉树是否为平衡二叉树

关于平衡二叉树这里有介绍：http://blog.csdn.net/wenqian1991/article/details/21889147

判断二叉树是否为平衡二叉树，就是判断其每个节点的左子树和右子树的高度差是否小于等于1。这里作为测试判断我们就借助以二叉查找树为目标对象，在AVL树插入环节去掉调整操作。

关键在于需要对每个节点的左右子树的高度差进行判断。

//计算节点的高度
int AvlTree::Height(AvlNode *node)
{
	int left, right;
	if (NULL == node)
		return -1;

	left = Height(node->leftchild);
	right = Height(node->rightchild);

	return (left > right) ? (left + 1) : (right + 1);
}

//递归测试每个节点
bool AvlTree::isBalanceTree(AvlNode *node)
{
	if (NULL == node)
		return true;

	int left = Height(node->leftchild);
	int right = Height(node->rightchild);

	if ((left - right > 1) || (left - right) < -1)
		return false;
	else
		return isBalanceTree(node->leftchild) && isBalanceTree(node->rightchild);
}

bool AvlTree::isBalanceTree(void)
{
	return isBalanceTree(Root);
}

其余代码及测试代码同，这里的插入操作应注释掉插入后调整操作部分。