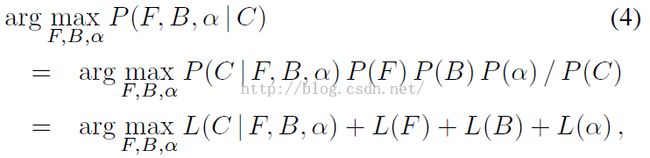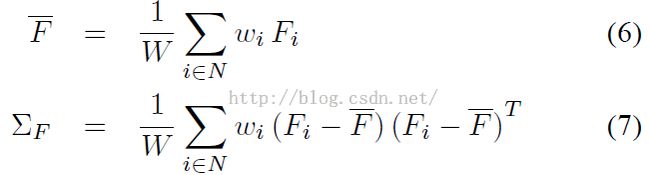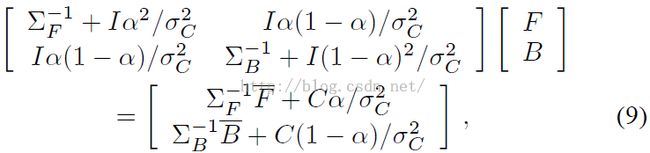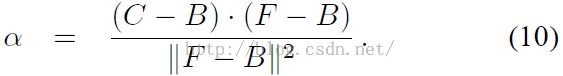图像处理(二十二)贝叶斯抠图-CVPR 2001
贝叶斯抠图
原文地址:http://blog.csdn.net/hjimce/article/details/47667947
作者:hjimce
一、相关理论
可能很多人会把图像分割和抠图混在一起。我的观点是图像分割和图像抠图的算法是完全不同的,图像抠图算法比较复杂,需要涉及到α值得求取问题,当然抠出来的精度也远远高于图像分割算法,当然速度不是一般的慢,所以基本上工程应用很难,商业软件抠图功能都是通过图像分割的算法实现的,比如一些升级版的grab cut算法。
图像抠图的英文单词又称之为:Matting。在图像里面前景色和背景色经过alpha融合后,得到一张图片:
其中F表示前景颜色值,B表示背景的颜色值。而C就是最后合成的结果。因此图像抠图就是已知C,求解F、B、alpha,这个可以说是一个无解的问题,因为未知的参数太多了,比方程组的个数还多,这样正是抠图的难点,于是大牛们想出了各种求解这个方程的方法,废话不多说。
这里我要讲的paper是2001年CVPR上的文献:《A Bayesian Approach to Digital Matting》。
paper的主页为:http://grail.cs.washington.edu/projects/digital-matting/image-matting/
先看一下文献的抠图效果:
感觉牛逼轰轰的样子,连头发都可以进行抠,然而其实这个算法的计算效率挺低的,到了后面你了解了这个算法,你就会知道速度有多么慢了。
二、贝叶斯抠图
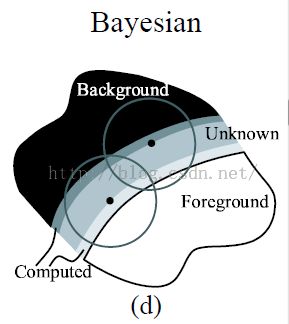
贝叶斯抠图是一种交互输入的抠图。也就是说图片C的一部分像素F、B、alpha值是已知的,这部分就是我们鼠标输入,确定的区域。然后还有一部分像素点的是F、B、alpha值未知的,抠图问题归结为:求解这部分未知的像素点的F、B、alpha值?
贝叶斯相关的理论我就不说了,只知道我们的目的是通过已知的C值,使得求解出来的F、B、alpha值,符合最大概率:
上面由相乘转换为相加,是通过取对数的方法,把乘法转换成加法,也就是:
同时,因为P(C)是常数项,因此被省略了。这个在学机器学习算法:朴素贝爷斯的时候,推导过程应该挺熟悉的,不解释。
因此呢,我们就是要求解最优的参数:F、B、alpha值,使得上面的式子的概率最大化。
回忆一下grab cut算法,grab cut算法通过高斯混合模型,为已知的前景和背景各建立了一个由5个高斯模型组成的高斯混合模型。理论上贝叶斯抠图也是要这样做。
然而贝爷斯为了保证空间的连贯性,就以每个未知像素的N个邻域点,进行聚类,为了简化起见,paper先假设,前景色只有一类,背景色也只有一类,记住这个只是对于一个像素点的N个领域点而言。至于N的值大小,paper选择200,也就是说每个未知的像素选择最近的200个进行相关的高斯建模。也就是说这200个邻域点,聚类模型前景和背景都是单高斯模型,这样我们就可以求得着200个邻域点属于这个高斯模型的概率了。
1、单高斯模型
下面就讲,N个邻域像素点的前景和背景都只有一个高斯模型时,公式4的求解过程:
(1)第一项:
我们知道公式(1),也就是:C=alpha*F+(1-alpha)*B,因此我们求解出来的参数F、B、alpha需要满足下面的公式:
也就是说,使得求解得到的参数,融合后的:
值,与真实值C之间的偏差,符合标准正太分布,其中上面的σ是标准差。上面公式是公式第一项的求解公式
(2)第二项L(F)
这一项就相当于计算,当前像素点属于前景的概率。我们可以通过用户输入的,已知的像素点,计算一个颜色值属于前景的概率。
连续性问题:我们构建每个像素点的邻域(N=200,默认)像素点的权重为:
I为当前像素点的邻接顶点,αi是I点的alpha值。
对于一个类,我们可以计算出其加权的平均颜色值F’,及其对应的协方差矩阵:
因此对于前景的高斯概率为:
(3)第三项L(B)
同样的对于背景,我们也选用同样的概率计算方法。唯一的区别是:
(4)第四项L(alpha)
对于透明度,paper先假设其为恒定的常数,这样公式4的最后一项可以省略。据此我们可以通过概率最大化方程,求解其偏导数,令其等于0。得到:
其中I是一个3*3的矩阵,因此我们可以通过求解上面6*6的线性方程,得到每个未知像素点的F、B值。
接着我们根据求得的F、B,假设F、B为常数,我们可以知道alpha的计算公式如下:
因此我们为了求解最大化概率方程,我们的步骤就是通过固定alpha的值,然后求解公式9得到F、B;接着固定F、B的值,求解公式10,得到alpha的值,如此循环迭代。对于alpha的初始化我们选择像素领域点的alpha的平均值。
2、像素点P的N邻域多类模型
我们上面的假设是,前景和背景进行聚类后,各自只有一个类,可想而知效果肯定很烂,grab cut算法就是假设前景和背景各有五个类,然后以高斯混合模型为基础。然而这篇paper,并不是以高斯混合模型为基础,而是以聚类后的背景和前景类之间,两两进行组合,然后选择使得上面的概率最大化的一对,这个paper原文如下:
假设像素点P的N个邻域点,进行建模聚类,如果前景和背景各聚为5个类,那么有5*5种组合,然后从这25种结果中,选择使得概率最大化的那个,这个每一种组合,就要求解一次,计算量很大。
看一下大体的流程:
for( p = 0 ; p < toSolveList.size() ;++p )
{
r = toSolveList[p].y, c = toSolveList[p].x;
GetGMMModel( r, c, fg_weight, fg_mean, inv_fg_cov, bg_weight, bg_mean, inv_bg_cov);
maxL = (float)-INT_MAX;
for(i=0;i<BAYESIAN_MAX_CLUS;i++)
for(j=0;j<BAYESIAN_MAX_CLUS;j++)
{
if(!Iteration)
InitializeAlpha( r, c, unsolvedmask );
else
InitializeAlpha( r, c, solveAgainMask );
for(iter=0;iter<3;++iter)
{
SolveBF( r, c, fg_mean[i], inv_fg_cov[i], bg_mean[j], inv_bg_cov[j] );
SolveAlpha( r, c );
}
L = computeLikelihood( r, c, fg_mean[i], inv_fg_cov[i], bg_mean[j], inv_bg_cov[j]);
if(L>maxL)
{
maxL = L;
fgClus = i;
bgClus = j;
}
}
这个算法网上有一大堆源码可以下载,这里就不进行代码讲解了。这个算法速度挺慢的,所以不要太过于迷你作者主页上的一些效果图。
**********************作者:hjimce 时间:2015.8.14 联系QQ:1393852684 地址:http://blog.csdn.net/hjimce 转载请保留本行信息********************
参考文献:
1、《A Bayesian Approach to Digital Matting》