背包问题详解
背包问题
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的体积和价值,在限定的总体积内,我们如何选择,才能使得物品的总价值最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算机复杂理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题,即在总体积不超过V的前提下,总价值是否能达到M?它是在1978年由Merkel和Hellman提出的。 背包问题简要的分为以下3种,还有一些都是这3种的变形以及组合。 01背包: 有N件物品和一个体积为V的背包。(每种物品均只有一件)第i件物品的体积是volume[i],价值是value[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包体积,且价值总和最大。
多重背包: 有N种物品和一个体积为V的背包。第i种物品最多有n[i]件可用,每件体积是volume[i],价值是value[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包体积,且价值总和最大。完全背包: 有N种物品和一个体积为V的背包,每种物品都有无限件可用。第i件物品的体积是volume[i],价值是value[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包体积,且价值总和最大。01背包
首先来看一下01背包,其他的背包问题都是在这个问题的基础上扩展而来的。 有N件物品和一个体积为V的背包。(每种物品均只有一件)第i件物品的体积是volume[i],价值是value[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包体积,且价值总和最大 01背包最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。有一个杭电的acm题目原型Coins 我们来看一下。
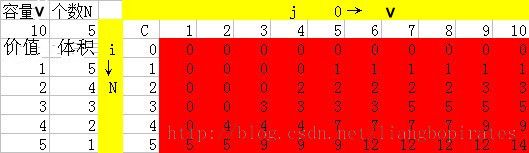
这个题目如何去解答呢?刚才也说了,对于只有一件的物品我们可以选择放,也可以选择不放。这就有点类似于DP的意思了。对于前i件物品组合的最优解肯定包含前i-1件物品组合的最优解,这就是最优子结构。其实DP是很灵活的,不一定非要满足3大条件才可以使用,但是必须满足的就是最优子结构性质。而且这个问题还满足重叠子问题性质,因为计算前i个和前i-1的最优解都要计算前i-2件物品组合的最优解,所以要用数组和自底向上。 你或许会说如果第i个物品的价值比第i-1个大,但是放不下了怎么办,拿掉第i个物品吗?NO,我们说的不是这个,我们说的是如果第i个物品的体积小于背包体积V,可以放可以不放.那么就比较前i-1个物品在V背包容量的最优解价值和前i-1的物品在容积为V减去第i个物品体积的背包容量的最优解加上第i个物品的价值,哪个大?如果前者大,那第i个物品就不放,如果后者大,那就放。因为如果要放第i个必须腾出位置来,来比较放入和不放入的价值。这样我们状态转换方程就出来了: p[i][j]=MAX{p[i-1][j-volume[i]]+value[i],p[i-1][j]}; 解释一下:p[i][j]代表前i件物品组合在容量为j的背包的最优解。将前i件物品放入容量为v的背包中这个子问题,若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品,那么问题就转化为“前i-1件物品放入容量为v的背包中,价值为p[i-1][v];如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下的容量为v-volume[i]的背包中”,此时能获得的最大价值就是p[i-1][j-volume[i]]再加上通过放入第i件物品获得的价值value[i]。 Ok,状态转换方程有了,开始编码呢?别着急,我们继续分析一下。根据刚才的方程,我们知道我们要求的值就是p[N][V]。根据刚才的分析我们知道我们要求1-V所有容量的最优解,而且这还要随着物品的一一加入而发生变化。我们遍历物品和容量二维的复杂度是O(NV)。举个例子,物品5个,背包容量是10。就是HDOJ刚才的例子。
对于第一行和第一列是要初始化为0(图中少了第一列),因为没有物品放入的最优解就是0,以及体积为0的背包不能放入物品最优解也是0;P[i][j]数组保存了1,2,3,4,5号物品依次选择后的最大价值. 这个最大价值是怎么得来的呢?从背包容量,为0开始,1号物品先试0,1,2,3,4的容量都不能放.所以置0,背包容量为5则里面放价值为1.这样,这一排背包容量为6,7,8....10的时候,最佳方案都是放价值1.则再看2号物品.当背包容量为4的时候,里面放入价值为2,背包容量为9的时候,放入2号物品的时候还有空余空间,很显然是2加上一个值了。加谁??很显然是9-4=5的时候.上一排 P5的最佳方案是1.所以,总的最佳方案是为3.再比如放4号物品的时候,当背包容量为2,放入价值为4的物品,当背包容量为5的时候,4加上上一排的p(5-2)的最佳方案为3,等于7.之后的9也是这样的道理。这样.一排一排推下去。最右下放的数据就是最大的价值了。
这样我们就可以来编码了
//Memory Limit Exceeded
#include <iostream>
using namespace std;
int main()
{
int V,N,Case;
int i,j;
int **p,*volume,*value;
cin>>Case;
while(Case--)
{
cin>>N;
cin>>V;
volume=new int[N+1];
value=new int[N+1];
for(i=1;i<=N;i++)
cin>>value[i];
for(i=1;i<=N;i++)
cin>>volume[i];
p=new int*[N+1];
for(i=0;i<=N;i++)
p[i]=new int[V+1];
for(i=0;i<=N;i++)
p[i][0]=0;
for(i=0;i<=V;i++)
p[0][i]=0;
for(i=1;i<=N;i++)
{
for(j=1;j<=V;j++)
{
if((volume[i]<=j)&&(p[i-1][j-volume[i]]+value[i]>p[i-1][j]))
p[i][j]=p[i-1][j-volume[i]]+value[i];
else
p[i][j]=p[i-1][j];
}
}
cout<<p[N][V]<<endl;
}
return 0;
}
这个提交上去得到Memory Limit Exceeded,说明内存占用太多了,辅助空间太多了。可以降低吗?对于保存价值和体积的空间是没法优化的,那么对于求最优解的数组可以优化到一维吗?先不说这个,这个算法不适应一种情况,那就是背包体积为0的时候,如果物品的体积也为0,价值反倒不是0,那么对于这个最优解就不是0了。纠结于这两种情况,改进算法是必然的。 这个问题和LCS的优化是类似的。对于求下一个状态,我们不是用整个NV数组,只用2V的空间,也就是2行的空间就足够了。这个可以利用一个2V空间的滚动数组来循环使用。值得一提的就是如果要找放入物品先后顺序路径,那就只能用NV空间的数组了。这种空间循环滚动使用的思想很有意思,类似的,大家熟悉的斐波那契数列,f(n) = f(n-1) + f(n-2),如果要求解f(1000),是不需要申请1000个大小的数组的,使用滚动数组只需申请3个空间f[3]就可以完成任务,甚至是2个空间。 对于求路径我们可以另外搞一个数组,类似LCS的。这里就不说了。 其实优化数组还可以做到一维数组,就是V个空间,因为我们用到的也不一定是2V空间,尽管占用了2行。这次我们求的时候遍历V-0,这个时候当我们求后半部分的时候就只和前半部分有关系,其实只要V个空间就好。 状态转移方程就是p[j]=MAX{p[j-volume[i]]+value[i],p[j]}; 和之前的的对比一下p[i][j]=MAX{p[i-1][j-volume[i]]+value[i],p[i-1][j]};发现只是第一维没了,没有关系。如果我们从V-0遍历,这个时候的伪代码
for i=1..N
for j=V..0
p[j]=MAX{p[j-volume[i]]+value[i],p[j]};
你会发现这两个状态方程的实质是一样的。我们求的p[j],就是第i次的p[i][j],而p[j-volume[i]]就是p[i-1][j-volume[i]],为啥呢?因为这个值必然是数组前边的,我们倒着求,那么这个时候前面的值就是上次求的,不就是i-1了吗?而中间变量p[j]也是上次求出来的即是p[i-1][j]。这个就一样了不是。 如果0-V遍历就错了,就变成了p[i][j]=MAX{p[i][j-volume[i]]+value[i],p[i][j]};和状态方程就不一样了。明白了吧。这个当然也是求不出路径的。优化以后空间复杂度降低了不少。 上代码
#include <iostream>
using namespace std;
int main()
{
int V,N,Case;
int i,j;
int *p,*volume,*value;
cin>>Case;
while(Case--)
{
cin>>N;
cin>>V;
volume=new int[N+1];
value=new int[N+1];
for(i=1;i<=N;i++)
cin>>value[i];
for(i=1;i<=N;i++)
cin>>volume[i];
p=new int[V+1];
for(i=0;i<=V;i++)
p[i]=0;
for(i=1;i<=N;i++)
{
for(j=V;j>=volume[i];j--) //这还减少了if判断,降低常数复杂度
{
if(p[j-volume[i]]+value[i]>p[j])
p[j]=p[j-volume[i]]+value[i];
else
p[j]=p[j];
}
}
cout<<p[V]<<endl;
}
return 0;
}
时间复杂度没有变化,空间复杂度降低到O(max(N,V))。 而且01背包还有一个问题,那就是满与不满。有时候让你求最大值,有时候会让你求恰好装满的最大值。这个时候该怎么办?我们看一下没要求恰好满的时候我们是如何初始化的,初始化价值都为0,是没有任何物品可以放入背包时的合法状态,是不存在非法状态的,所有的都是合法状态,因为可以什么都不装,这个解就是0。然而如果要求恰好装满的时候,只有容量为0的背包可能被价值为0的nothing“恰好装满”,初始化合法状态只有背包容量V为0的时候才可以初始化为0,其他的背包容量都要初始化为一个负无穷,对于二维的数组只要第一列初始化为0,一维的数组只要P[0]=0,其他都初始化负无穷(如果要求的是最小值,初始化为正无穷)。要注意的是改变初始化以后最后一个值是恰好装满的最大值,如果不能恰好装满,那肯定是一个负数(前提是初始化的负数足够大),而且对于恰好装满的的初始化情况的不要求满的最大值是0-v背包容量的最大值。即是最后一行的MAX。完全背包
有N种物品和一个体积为V的背包,每种物品都有无限件可用。第i件物品的体积是volume[i],价值是value[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包体积,且价值总和最大。 虽然是无限使用,但是用到的还是有限个,即V/volume[i]。 这和01背包的区别就是求解每一种物品的时候状态是多个,即V/volume[i],这样我们可以把第i种物品分成V/volume[i]份取出来,每份一件。这样就和01没有了区别了。可以变换数组,也可以直接增加一个循环,这样时间复杂度就增加了。对于取多少也可以利用二进制拆分,取的时候取 1 2 4 ...。详细的做法和代码的编写见下面的多重背包,因为多重的解法和这个是一样的。
我们在这来讲一个完全背包的一个优化算法。和01背包问题的时候差不多,状态转换方程都是一样的,就是遍历的时候变成了从0-V而已。 for i=1..N for j=0..V p[j]=MAX{p[j-volume[i]]+value[i],p[j]}; 为啥呢?因为之前的01背包要从V-0,是要找前一个i-1,因为每一个物品只有一个,放i物品的时候之前是没有i物品放入的。而现在不需要,因为每一个物品有很多次,这样我们就不必再找i-1,就找i就好了,我们允许放过i物品的基础上的背包再放一个i物品。即是 p[i][j]=MAX{p[i][j-volume[i]]+value[i],p[i][j]};j是越来越大,相当于加入多个i物品。 也可以这么理解。外层循环放0-V,对于每一个容量i我们要求出其能放的最大值。这样物品可以依次放如,循环的时候物品也可以重复放入。而且这两个循环是可以调换的,就变成了这样。
#include <iostream>
using namespace std;
int main()
{
int V,N,Case;
int i,j;
int *p,*num,*value;
cin>>Case;
while(Case--)
{
cin>>N;
cin>>V;
num=new int[N+1];
value=new int[N+1];
for(i=1;i<=N;i++)
cin>>value[i];
for(i=1;i<=N;i++)
cin>>num[i];
p=new int[V+1];
for(i=1;i<=V;i++)
p[i]=0;
for(i=1;i<=N;i++)
{
for(j=num[i];j<=V;j++) //提升一下
{
if(p[j-num[i]]+value[i]>p[j])
p[j]=p[j-num[i]]+value[i];
else
p[j]=p[j];
}
}
cout<<p[V]<<endl;
}
完全背包问题有一个很简单有效的优化:若两件物品i、j满足volume[i]<=volume[j]且value[i]>=value[j],则将物品j去掉,不用考虑。这个优化的正确性显然:任何情况下都可将价值小体积高的j换成物美价廉的i,得到至少不会更差的方案。对于随机生成的数据,这个方法往往会大大减少物品的件数,从而加快速度。然而这个并不能改善最坏情况的复杂度,因为有可能特别设计的数据一件物品也去不掉。多重背包
有N种物品和一个体积为V的背包。第i种物品最多有num[i]件可用,每件体积是volume[i],价值是value[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包体积,且价值总和最大。 这和01背包的区别就是多了一个num[i],这样我们可以把第i种物品分成num[i]份取出来,每份一件。这样就和01没有了区别了。可以变换数组,也可以直接增加一个循环,这样时间复杂度就增加了。值得注意的是虽然说是可以拿0 1 2 3 4 ..但是要一件一件的拿,不是先拿1件,再拿2件,那就变成拿3件了!
#include <iostream>
using namespace std;
const int INFINITY=-100000;
int main()
{
int V,N,Case;
int i,j;
int *p,*num,*value,*volume;
cin>>Case;
while(Case--)
{
cin>>N;
cin>>V;
num=new int[N+1];
volume=new int[N+1];
value=new int[N+1];
for(i=1;i<=N;i++)
cin>>value[i];
for(i=1;i<=N;i++)
cin>>volume[i];
for(i=1;i<=N;i++)
cin>>num[i];
p=new int[V+1];
for(i=1;i<=V;i++)
p[i]=INFINITY;
p[0]=0;
for(i=1;i<=N;i++)
{
for(k=1;k<=num[i];k++)
{
for(j=V;j>=volume[i];j--) //这还减少了if判断
{
if(p[j-volume[i]]+value[i]>p[j])
p[j]=p[j-volume[i]]+value[i];
else
p[j]=p[j];
}
}
}
cout<<p[V]<<endl;
}
return 0;
}
不过代码可以变成这样,把0-num[i]的循环放到里面。因为调换了循环的先后,这个时候对于V-0个背包容量可以先拿一个,然后再拿一个,相当于第二次执行的时候是拿两个,因为之前的一个是拿过的,总共是拿两个。这个和刚才不同,刚才是对于每一个num[i],遍历V,那样的话不可以用k乘,细细体会一下两者的不同。
for(i=1;i<=N;i++)
{
for(j=V;j>=value[i];j--)
{
for(k=0;k<=num[i];k++)
{
if((j>=k*value[i])&&(p[j-k*value[i]]+k*value[i]>p[j]))
p[j]=p[j-k*value[i]]+k*value[i];
else
p[j]=p[j];
}
}
}
这样时间复杂度变成了O(NMC),C是物品的数量。可不可以改变呢?我们可以利用二进制拆分,利用了一种二进制思想:即任何数字都可以表示成若干个2^k数字的和,例如7可以用1+2+2^2表示;这很好理解,因为任何正数都可以转成二进制,二进制就是若干个“1”(2的幂数)之和。就像15个1分成1 2 4 8,这几个数的组合的值肯定和15个1组合的来的值是一样的。类似的1,2,4,...,2^(k-1),n-2^k+1,且k是满足n-2^k+1>0的最大整数。 举例 7拆分1 2 4 。kmax=2,因为7-8+1=0。拆分成 1 2 ,此时最后一个值是n-2^k+1=7-4+1=4。8拆分成1 2 4 ,最后一个是8-8+1=1.。 代码
#include<iostream>
using namespace std;
int main()
{
int N,V;
int i,j,m;
float k,n;
n=2;
int *p,*num,*value,*volume;
while(cin>>N>>V)
{
if(N==0&&V==0)
break;
number=0;
num=new int[N+1];
volume=new int[N+1];
value=new int[N+1];
for(i=1;i<=N;i++)
cin>>value[i];
for(i=1;i<=N;i++)
cin>>volume[i];
for(i=1;i<=N;i++)
cin>>num[i];
p=new int[V+1];
for(i=0;i<=V;i++)
p[i]=0;
for(i=1;i<=N;i++)
{
for(k=1;k<num[i]+1;k*=2)
{
if(2*k>num[i]+1)//这个是不满足2^k的最后一个拆分
{
k=num[i]+1-k;
for(j=V;j>=k*volume[i];j--)
{
if(p[j-k*volume[i]]+k*value[i]>p[j])
p[j]=p[j-k*volume[i]]+k*value[i];
else
p[j]=p[j];
}
}
else
{
for(j=V;j>=k*volume[i];j--)
{
if(p[j-k*volume[i]]+k*value[i]>p[j])
p[j]=p[j-k*volume[i]]+k*value[i];
else
p[j]=p[j];
}
}
}
}
cout<<p[V]<<endl;
}
return 0;
}
这样时间复杂度变成了O(NMlgC),好一些。不过还不够好,因为多重背包问题是包含一次背包和完全背包的,这两个问题要剪枝分类处理。这个完全背包就是如果满足value[i]*num[i]>=V,这个时候就和完全背包没有区别了,虽然是多重但是完全背包也是有限,如果满足这个条件就说明可以用完全背包来解,毕竟完全背包要比多重背包的复杂度低,是O(NV)。满足num[i]=1就可以用01背包来解决,这个就不贴代码了,很简单的,无非是多几个循环语句。剪枝是非常有效的。 听说楼教主的八题之中有O(NM)时间复杂度的算法,找了资料看了看,是利用单调递增序列来求解的。 什么是单调递增序列呢?至于单调队列,就是一个双端队列,在队首(f)出队,在队尾(b)出队入队,我们要维护整个队列的元素是单调的,比如,我们要动态查询从左向右的区间的最大值,那么我们就要在队列中维护一个单调递减的序列,从左向右枚举,队列的元素还有一个id值,代表这个元素在原序列中的位置,然后左边的元素如果不在范围内了,就判断队首的元素id是否是这个左边的id,是的话就出队,否则就不管。关于元素入队,首先判断入队的元素是否小于于队尾的元素(保证队列单调递减),如果不小于,那么弹出队尾元素,直到队尾元素大于入队元素或者队列为空,扔掉就不管他。我们要求的仅仅是最大值而已。看起来整个的操作时间是需要O(N),但是平摊的每一个元素身上就是O(1),而且取队首元素的时间也是O(1)。 就是说根据容量volume[i]将0-V所有值划分(d=j/volume[i])到d(0<=d<volume[i])中,体积的遍历就变成了遍历0-volume[i],体积等于k*volume[i]+d(k>0)。对于不同的状态划分不同的解决,利用一个单调序列(主队列和辅助队列)解决,这样可以把O(VC)变成O(V),可是具体的我也想不明白。如果有人很明白,请告诉我。这个地方先暂时搁下。
转载请注明出处http://blog.csdn.net/liangbopirates/article/details/9750463其他背包
混合背包,如果将01、完全、多重混合起来。也就是说,有的物品只可以取一次(01背包),有的物品可以取无限次(完全背包),有的物品可以取的次数有一个上限(多重背包)。应该怎么求解呢?无非是分类求解罢了,判断是哪一种,然后分别给出循环和循环顺序,分别调用状态转换方程就OK了。 还有二维费用背包,依赖背包,分组背包,在这里就不多说了。详见背包九讲。