矩阵快速幂--学习笔记

     据说，矩阵快速幂在递推式优化上相当神奇，而且效率很高。。。

     进一步理解矩阵快速幂，强力建议大神博客：http://www.matrix67.com/blog/archives/276

　　两矩阵相乘，朴素算法的复杂度是O(N^3)。如果求一次矩阵的M次幂，按朴素的写法就是O(N^3*M)。既然是求幂，不免想到快速幂取模的算法，这里有快速幂取模的介绍，a^b %m 的复杂度可以降到O(logb)。如果矩阵相乘是不是也可以实现O(N^3 * logM)的时间复杂度呢？答案是肯定的。

　　先定义矩阵数据结构：　　

struct Mat {
    double mat[N][N];
};

　　O(N^3)实现一次矩阵乘法

Mat operator * (Mat a, Mat b) {
    Mat c;
    memset(c.mat, 0, sizeof(c.mat));
    int i, j, k;
    for(k = 0; k < n; ++k) {
        for(i = 0; i < n; ++i) {
            if(a.mat[i][k] <= 0)  continue;   //不要小看这里的剪枝，cpu运算乘法的效率并不是想像的那么理想（加法的运算效率高于乘法，比如Strassen矩阵乘法）
            for(j = 0; j < n; ++j) {
                if(b.mat[k][j] <= 0)    continue;    //剪枝
                c.mat[i][j] += a.mat[i][k] * b.mat[k][j];
            }
        }
    }
    return c;
}

 

　　下面介绍一种特殊的矩阵：单位矩阵

很明显的可以推知，任何矩阵乘以单位矩阵，其值不改变。

有了前边的介绍，就可以实现矩阵的快速连乘了。

Mat operator ^ (Mat a, int k) {
    Mat c;
    int i, j;
    for(i = 0; i < n; ++i)
        for(j = 0; j < n; ++j)
            c.mat[i][j] = (i == j);    //初始化为单位矩阵

    for(; k; k >>= 1) {
        if(k&1) c = c*a;

        a = a*a;
    }
    return c;
}

举个例子:

　　求第n个Fibonacci数模M的值。如果这个n非常大的话，普通的递推时间复杂度为O(n)，这样的复杂度很有可能会挂掉。这里可以用矩阵做优化，复杂度可以降到O(logn * 2^3)

如图：

A = F(n - 1), B = F(N - 2)，这样使构造矩阵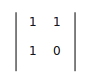的n次幂乘以初始矩阵得到的结果就是。

因为是2*2的据称，所以一次相乘的时间复杂度是O(2^3)，总的复杂度是O(logn * 2^3 + 2*2*1)。

 

zoj上的一道例题: zoj 2853 Evolution.

这道题都不用考虑怎么去构造能够实现有效运算的矩阵。直接修改单位矩阵就可以。比如P(i, j) = 0.5，则mat[i][j] += 0.5,mat[i][i] -= 0.5; 然后求T*mat^M,(T表示原始的population序列，相当于1*n的矩阵)

ps:这道题不加剪枝的话还是会挂掉 -_-!

渣代码 :3S+ 过得，很水 T_T

 

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 210;

struct Mat {
    double mat[N][N];
};

double num[N];
int n, m;
Mat a;

void init() {
    int i, j, q;
    double x;
    for(i = 0; i < n; ++i)
            for(j = 0; j < n; ++j)
                a.mat[i][j] = (i == j);
    for(i = 0; i < n; ++i) {
        scanf("%lf", num + i);
    }
    scanf("%d", &q);
    while(q--) {
        scanf("%d%d%lf", &i, &j, &x);
        a.mat[i][i] -= x;
        a.mat[i][j] += x;
    }
}

Mat operator * (Mat a, Mat b) {
    Mat c;
    memset(c.mat, 0, sizeof(c.mat));
    int i, j, k;
    for(k = 0; k < n; ++k) {
        for(i = 0; i < n; ++i) {
            if(a.mat[i][k] <= 0)  continue;    //***
            for(j = 0; j < n; ++j) {
                if(b.mat[k][j] <= 0)    continue;    //***
                c.mat[i][j] += a.mat[i][k] * b.mat[k][j];
            }
        }
    }
    return c;
}

Mat operator ^ (Mat a, int k) {
    Mat c;
    int i, j;
    for(i = 0; i < n; ++i)
        for(j = 0; j < n; ++j)
            c.mat[i][j] = (i == j);

    for(; k; k >>= 1) {
        if(k&1) c = c*a;

        a = a*a;
    }
    return c;
}

int main() {
    //freopen("data.in", "r", stdin);

    int i;
    double res;

    while(~scanf("%d%d", &n, &m)) {
        if(!n && !m)    break;
        init();
        a = a^m; res = 0;
        for(i = 0; i < n; ++i) {
            res += num[i]*a.mat[i][n-1];
        }
        printf("%.0f\n", res);
    }
    return 0;
}

ps:以上内容是本菜参考各种资料整理的，欢迎转载，请注明出处。http://www.cnblogs.com/vongang/archive/2012/04/01/2429015.html