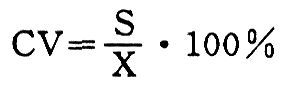统计学 学习笔记 （三）—— 掌握数据的整体状态 数据的变异性

数据的变异性

    从上节的分析可看到，均值、中值、众数等可以反映数据组的集中趋势。但为了了解数据的变异性，光有这些集中趋势量度是不够的。比如下面的例子：
7, 6, 3, 3, 1
3, 4, 4, 5, 4
4, 4, 4, 4, 4
    从集中趋势来看，这三组的均值都是4。但明显它们之间的数值不一样。
    数据的变异性（散布，离散度）可看作是对不同数值间的差异性的度量。直观来说，上面第一组数据组数值之间相差比较大，而第三组数据组中任意数值之间相等无差异。而当我们在比较“数值之间的差异”时，其实是在把组内的每个数值与一个“特定的数值”进行比较。这个“特定的数值”，通常情况下其实就是均值。从下面反映数据变异性的指标，也能印证这个观点。
    反映数据变异性的常用指标有极差、标准差和方差。当想比较两组数据的变异性时，若两组数据的单位不同，还可以通过变异系数来反映其差别。
    极差 （全距，range）：数据组中的最大值减去最小值。是对变异性最笼统的测量。通过极差可以了解数值之间彼此差异的程度，掌握数据组中从最小值到最大值之间的距离。
    标准差 （standard deviation，s）：数据组中所有数值与均值的平均距离。表示数据组中变异性的平均数量。公式为[Wikipedia, standard deviation]：

    关于为什么要选择这样一个公式计算标准差，《爱上统计学》和《医用统计方法》中给出了若干观点，个人认为非常清楚明了：
•    如果直观地根据标准差的定义，将每个数值与均值的差值累加起来，通常情况下这个差值都等于0。
•    为了消除差值相加时的负号，先对每个差值进行平方，然后再相加。
•    为了求得差值的平均值，需要对上述得到的结果除以差值的个数。这儿采用n-1而不是n，一方面是为了做更保守的估计（这样计算的标  准差会比实际大一点，不容易因低估差异而出错）；另一方面，一般都是在样本而不是总体上来计算标准差，梳理统计理论证明，这样求得的标准差是总体标准差的无偏估计。
•    最后，为了让标准差回到开始时的计算单位，对上面的结果进行开方。
    由于标准差是根据均值来计算的，因此标准差对极值也比较敏感。
    变异系数 (coefficient of variation，CV)：标准差对均值的百分比。由于标准差的单位和数据值的单位相同，若想比较两组不同单位的数据的变异性大小，就无法直接比较其标准差了。但若使用变异系数，得到的是无单位的百分比，就可以让不同的数据组相互比较。

 

    方差 （variance）：标准差的平方。