Matlab曲线拟合

最近学习了一哈Matlab，才发现数学很重要那。。。

百度一哈拟合，所谓拟合是指已知某函数的若干离散函数值{f1,f22,...,fn}，通过调整该函数中若干待定系数f(λ1,λ2,...,λn),使得该函数与已知点集的差别（最小二乘意义）最小。如果待定函数是线性，就叫线性拟合或者线性回归（主要在统计中），否则叫做非线性拟合或者非线性回归、表达式也可以是分段函数，这种情况下叫做样条拟合。

形象的说，拟合就是把平面上一系列的点，用一条光滑的曲线连接起来，因为有这条曲线有无数种可能，从而有各种拟合的方法。拟合的曲线一般可以用函数表示，根据这个函数的不同有不同的拟合名字。

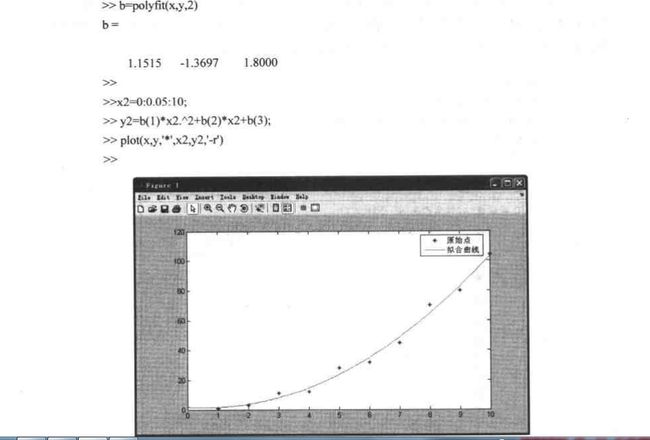
最佳拟合被解释为在数据点的最小误差平方和，且所用的曲线先定为多项式时，那么曲线拟合是相当简捷的，数学上称为多项式的最小二乘曲线拟合，这个最容易懂了，看一下MATLAB7.0基础教程上的例子就好了。在Matlab中使用polyfit(x,y,n)命令用最小二乘法对所给数据进行N阶多项式拟合，得到拟合多项式p(x)，使得p(x(i))约等于y(i).具体命令看matlab帮助手册即可，书中的例子如下

选用二阶多项式来拟合

可以看出所得到的拟合曲线跟元数据的拟合程度相接近，但不是N越大越好。

在日常中，问题常常不是这么简单，我们需要设置参数来求出我们所需的拟合曲线函数，这个时候使用fitoptions函数来帮助我们，最开始就是遇到这个函数不懂浏览了很多网页。。。fitoptions有很多种形式可根据帮助文档来理解，在帮助文档里有一个例子

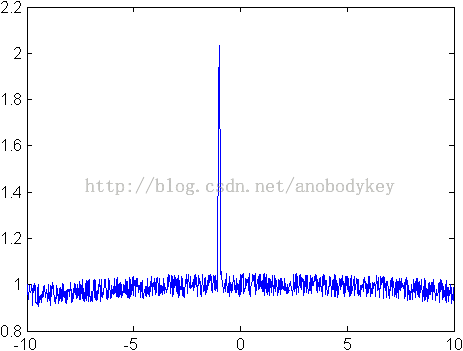
这个是原始数据

我们要拟合出该曲线函数,形似高斯函数

m=fitoptions（'Method','NonlinearLeastSquares','Upper',[Inf,Inf,Inf,Inf],'Lower',[0,0,0,0],'StartPoint',[1,1,1,1]）;

f=fittype('a+b*exp(-(x-c)/d)^2','options',m);

[h,g]=fit(x,y,f);

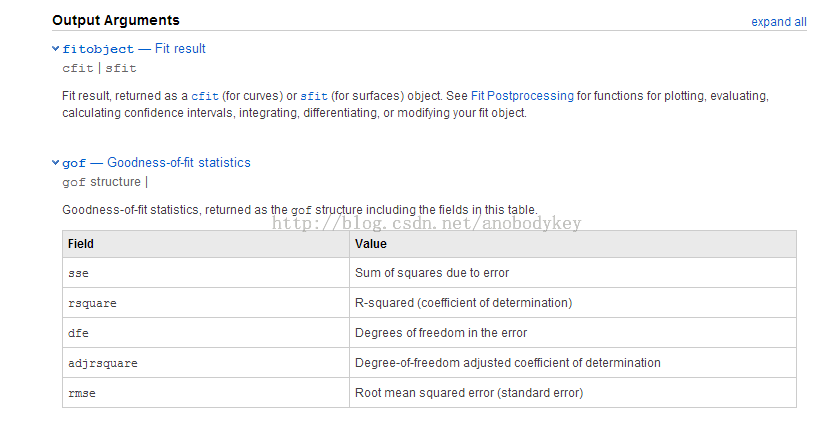
在fitoptions中，Method参数为NonlinearLeastSquares，非线性最小平方和，Upper，Lower，startPoint分别指明了各个系数的上限，下限以及初始默认值，即对应下面我们的高斯函数的系数a,b,c,d的取值，通过fit函数来得到各个系数的取值以及平方差的值，在帮助文档中可知。

还是多看帮助文档好，而且数学要学好。。。