Trie树|字典树的简介
其基本性质可以归纳为:
1. 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。
其基本操作有:查找 插入和删除,当然删除操作比较少见.我在这里只是实现了对整个树的删除操作,至于单个word的删除操作也很简单.
搜索字典项目的方法为:
(1) 从根结点开始一次搜索;
(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
其他操作类似处理.
举个简单的例子。
给你100000个长度不超过10的单词。对于每一个单词,我们要判断他出没出现过,如果出现了,第一次出现第几个位置。
这题当然可以用hash来,但是我要介绍的是trie树。在某些方面它的用途更大。比如说对于某一个单词,我要询问它的前缀是否出现过。这样hash就不好搞了,而用trie还是很简单。
现在回到例子中,如果我们用最傻的方法,对于每一个单词,我们都要去查找它前面的单词中是否有它。那么这个算法的复杂度就是O(n^2)。显然对于100000的范围难以接受。现在我们换个思路想。假设我要查询的单词是abcd,那么在他前面的单词中,以b,c,d,f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的,在以a开头中的单词中,我们只要考虑以b作为第二个字母的……这样一个树的模型就渐渐清晰了……
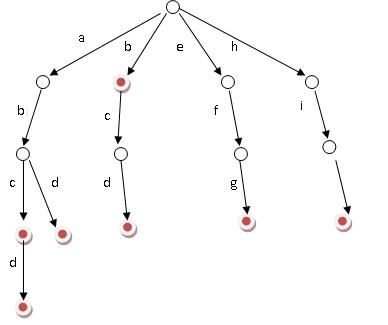
假设有b,abc,abd,bcd,abcd,efg,hii这6个单词,我们构建的树就是这样的
对于每一个节点,从根遍历到他的过程就是一个单词,如果这个节点被标记为红色,就表示这个单词存在,否则不存在。
那么,对于一个单词,我只要顺着他从跟走到对应的节点,再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色,就相当于插入了这个单词。
这样一来我们询问和插入可以一起完成,所用时间仅仅为单词长度,在这一个样例,便是10。
我们可以看到,trie树每一层的节点数是26^i级别的。所以为了节省空间。我们用动态链表,或者用数组来模拟动态。空间的花费,不会超过单词数×单词长度。
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int num_chars = 26;
class Trie {
public:
Trie():root(NULL){};
Trie(Trie& tr);
int search(const char* word, char* entry ) const;
int insert(const char* word, const char* entry);
int remove(const char* word, char* entry);
private:
struct Trie_node
{
char* data;
Trie_node* branch[num_chars];
Trie_node();
}* root;
};
Trie::Trie_node::Trie_node()
{
data = NULL;
for (int i=0; i<num_chars; ++i)
branch[i] = NULL;
}
int Trie::search(const char* word, char* entry ) const
{
int position = 0;//依旧是从根开始找
char char_code;
Trie_node *location = root;
while( location!=NULL && *word!=0 )
{
if (*word>='A' && *word<='Z')
char_code = *word-'A';
else if (*word>='a' && *word<='z')
char_code = *word-'a';
else return 0;
location = location->branch[char_code];
position++;
word++;
}
if ( location != NULL && location->data != NULL )
{
strcpy(entry,location->data);
return 1;
}
else return 0;
}
int Trie::insert(const char* word, const char* entry)
{
int result = 1, position = 0;
if ( root == NULL ) root = new Trie_node;
char char_code;//标识Trie_node节点中branch[char_code];
Trie_node *location = root;//赋值root,从根节点开始查找插入
while( location!=NULL && *word!=0 )
{
//考虑大小写两种情况
if (*word>='A' && *word<='Z')
char_code = *word-'A';
else if (*word>='a' && *word<='z')
char_code = *word-'a';
else return 0;
//如果以前插入的word不包含这个字符,则创建新的节点
if( location->branch[char_code] == NULL )
location->branch[char_code] = new Trie_node;
location = location->branch[char_code];
position++;
word++;
}
//如果当前要插入的word在树中已有 ,返回result=0;
if (location->data != NULL)
result = 0;
//如果不存在,进行如下操作
else {
location->data = new char[strlen(entry)+1];
strcpy(location->data, entry);
}
return result;
}
int main()
{
Trie t;
char entry[100];
t.insert("aa", "DET");
t.insert("abacus","NOUN");
t.insert("abalone","NOUN");
t.insert("abandon","VERB");
t.insert("abandoned","ADJ");
t.insert("abashed","ADJ");
t.insert("abate","VERB");
t.insert("this", "PRON");
if (t.search("this", entry))
cout<<"'this' was found. pos: "<<entry<<endl;
if (t.search("abate", entry))
cout<<"'abate' is found. pos: "<<entry<<endl;
if (t.search("baby", entry))
cout<<"'baby' is found. pos: "<<entry<<endl;
else
cout<<"'baby' does not exist at all!"<<endl;
if (t.search("aa", entry))
cout<<"'aa was found. pos: "<<entry<<endl;
system("PAUSE");
return 0;
}