HDU 4565So Easy!2012长沙邀请赛A题(共轭构造+矩阵的快速幂)
So Easy!
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 910 Accepted Submission(s): 247
Problem Description
A sequence S
n is defined as:
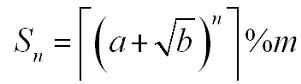
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n.
You, a top coder, say: So easy!

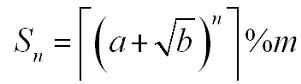
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n.
You, a top coder, say: So easy!

Input
There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2
15, (a-1)
2< b < a
2, 0 < b, n < 2
31.The input will finish with the end of file.
Output
For each the case, output an integer S
n.
Sample Input
2 3 1 2013 2 3 2 2013 2 2 1 2013
Sample Output
4 14 4
题目大意:
题目意思很好懂,主要是小数的n次方不好处理,如果简单的将整数小数隔离开来,然后对整数对m求余。会有漏洞,前面的数据再乘上后面的小数会产生新的数字,对结果有影响。
解题思路:下来之后看了下题解,都是直接找一个共轭的(a-sqrt(b))^n一加便组成了整数。以前一直以为共轭只能存在于复数中。a+bi与a-bi共轭之类的。看来还要请教一下自己的高中老师。
下面是自己的推论,组成了整数之后一切都好办了,然后往下推,可以得到一个间接递推公式,然后转化成矩阵。
快速幂的思想:我也是第一次用这个,所以说下感想,主要是普通的递推或者直接矩阵转换超时。所以用快速幂来求解。比如某个矩阵的31次方,可以写成(1+2*(1+2*(1+2*(1+2)))),只需要八次左右的运算,就可以了,首先31&1=1,那么就分解一个1出来,然后p*ret,然后就变成了偶数30,将p矩阵变成p^2,n变成15,&1=1直接用p*ret这时候p已经是p^2了,如此反复最后便可以把它求出来。 和求一个数的快速幂是一样的原理。
题目地址:So Easy!
AC代码:
#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#include<cstdio>
using namespace std;
__int64 a,b,n,m;
__int64 ret[2][2],p[2][2],tmp[2][2];
void init()
{
ret[0][0]=2*a;
ret[0][1]=-(a*a-b);
ret[1][0]=1;
ret[1][1]=0;
p[0][0]=2*a;
p[0][1]=-(a*a-b);
p[1][0]=1;
p[1][1]=0;
}
void cal1() //矩阵的平方!&1
{
int i,j,k;
for(i=0;i<2;i++)
for(j=0;j<2;j++)
{
tmp[i][j]=p[i][j];
p[i][j]=0;
}
for(i=0;i<2;i++)
for(j=0;j<2;j++)
for(k=0;k<2;k++)
p[i][j]=(p[i][j]+tmp[i][k]*tmp[k][j])%m;
}
void cal2() //矩阵的乘法&1
{
int i,j,k;
for(i=0;i<2;i++)
for(j=0;j<2;j++)
{
tmp[i][j]=ret[i][j];
ret[i][j]=0;
}
for(i=0;i<2;i++)
for(j=0;j<2;j++)
for(k=0;k<2;k++)
ret[i][j]=(ret[i][j]+tmp[i][k]*p[k][j])%m;
}
void fastmi()
{
n-=2;
while(n)
{
if(n&1) cal2();
cal1();
n>>=1;
}
}
int main()
{
while(~scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&m))
{
if(n==1)
{
printf("%I64d\n",2*a%m);
continue;
}
init();
fastmi();
//C1=2*a C0=2
printf("%I64d\n",((ret[0][0]*2*a+ret[0][1]*2)%m+m)%m);
}
return 0;
}
