哈夫曼编码正确性之屌丝证明法
哈夫曼编码是数据结构中比较基础的东西。最近遇到一个类似哈夫曼编码的问题,解法却截然不同。
问题A君:N堆石子排成一列,两两合并成一堆,只能相邻的合并。合并的代价为两堆石子个数之和。总的代价为所有中间结果之和。
求最小总代价。
也就是有次序的哈夫曼树。
对比两个问题后,开始思考哈夫曼编码的正确性问题。
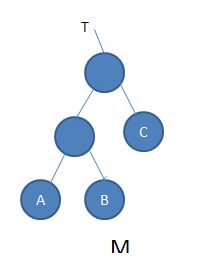
回顾一下哈夫曼编码:
哈夫曼编码的构造代价为
Cost=所有叶子节点代价*叶子节点的层数.
哈夫曼编码用的是一种贪心的方法来构造最小代价树,如下:
1.N个节点,取最小代价的两个节点合并为一个,新的节点代价为两个子节点代价之和
2.通过1步骤,变为N-1个节点.重复1过程,直到只剩一个节点.
问题A君如果用哈夫曼的贪心算法,优先合并最小和,得出的并不是最优解.
我开始思考,这种代价与哈夫曼建树的代价有什么区别.
为什么哈夫曼树的cost能用贪心,而这种树的cost不能.
首先从哈夫曼编码的正确性入手,思考为什么贪心是最优的。
哈夫曼编码的正确性证明:
1. 代价小的节点,层次一定最大.
用反证法.
如果A,B两个节点不是代价最小的,如,A>C>B.
那么交换A,C的位置,明显代价会减小C-A>0;
也就是交换后代价会变小.即当前不是最优解.
上面表明,如果得到的树是最优的,那么一定节点越小,层次越大.
通过这一步的证明,再看问题A。由于构造顺序是固定的,故不满足这一条定律.由此也可以解释,为什么贪心的方法不适用于他.
2. 下面证明,越早构造合并的节点,层次越大.
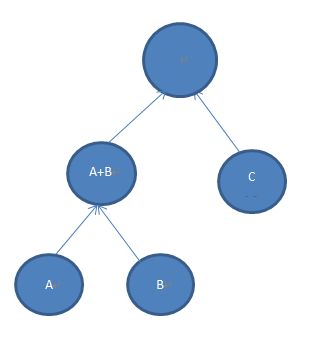
假设A,B,C,D,E五个节点,代价为A<B<C<D<E.
按照贪心的规则,首先会合并A,B两个节点,得到A+B.
我们用C(A)表示A的层次.
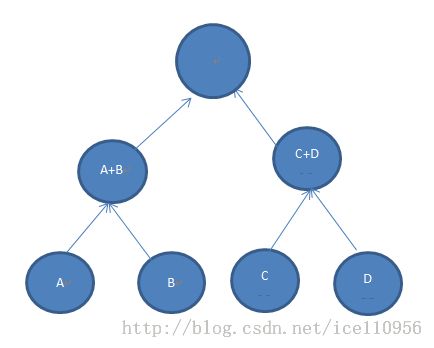
因为在A,B构造之后,所有的节点权值之和只可能大于A+B.
也就是C+D+E>E+D>C+E>C+D>A+B.
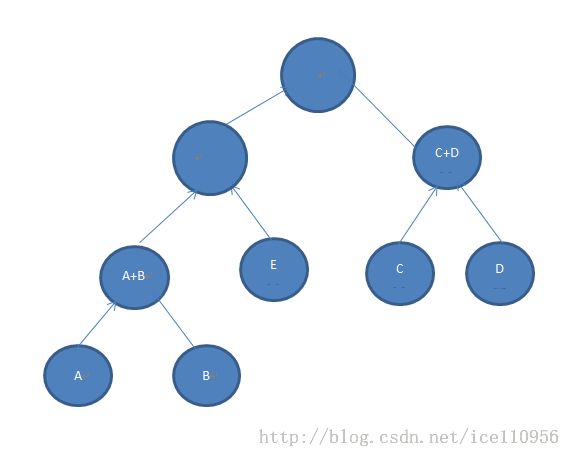
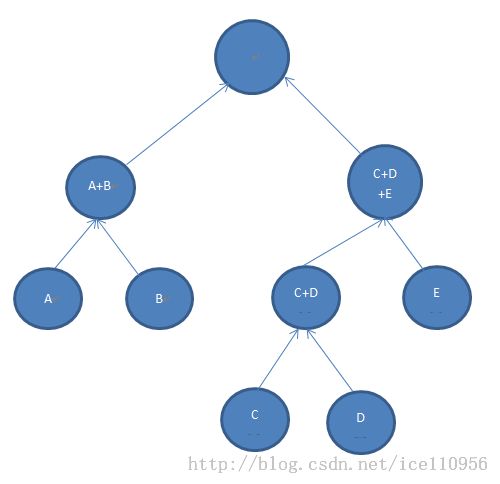
按照贪心规则,A+B或跟单个节点C,E,合并;或跟C+D合并,得到如下树形.
此时C(A),C(B)>=C(C).
而下图这种树形是不可能构造出来的.
也就证明了C(A),C(B)>=C(C).
上面用屌丝的推理方式。之所以这样称呼,因为证明并不是基于严格的数学推导。
在证明的过程中,也顺便得出了,问题A,顺序最小代价树的非贪心特性.小结一下:
1.由于顺序是固定的,所以越小的不一定层次越大,因为其转化为更优解也许不满足次序.
2.还是由于次序固定,先合并的层次不一定最大.
那么问题A用什么方法呢?想到了动态规划。
下面用动态规划解决上面的问题:
由于最后生成树一定是两个子树合并,有n-1种情况,即:
用f(1,N)表示1到N节点的最优解,则得到我们的动态规划递推公式:
F(1,N)=max(f(1,1)+f(2,N),f(1,2)+f(3,N),………f(1,N-1)+f(N,N)).
F(i,i)=A[i];
最后编码解决上述问题:
int max(int left,int right)
{
int maxx=-1;
for (int i=left;i<right;i++)
{
if (A[left][i]+A[i+1][right]>maxx)
maxx=A[left][i]+A[i+1][right];
}
return maxx;
}
int f()
{
for (int L=1;L<=N;L++)
{
for (int i=1;i<=N-L+1;i++)
{
A[i][i+L-1]=max(i,i+L-1);
}
}
}