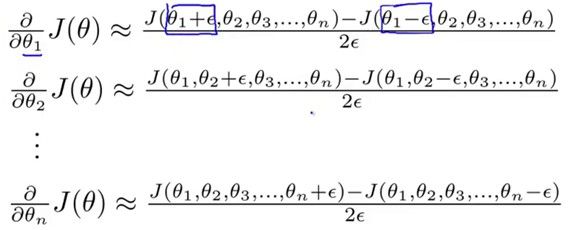Standford机器学习 神经网络的学习（Neural Network Learning）

        上一讲讲了神经网络的表示，神经网络中，从前一层映射到后一层的需要有个一个权重矩阵Theta和激活函数，映射后可以得到该层神经元的activation。如何来学习Theta是本讲要解决的内容。

首先，对于一个分类问题，如果是两类问题，输出层只需要有一个神经元，输出1为正类，输出0为负类。而对于多类的问题，需要有多个神经元。定义一个神经网络，如下：

 

它的输出是一个向量，如图，假设要分成4类，向量的对应类别下标为1，输出可以表示成

 

 

根据上一讲神经网络的表示，和逻辑回归的估价函数类似（神经网络就是把每个神经元的估价函数相加得到的），可以得出如下的估价函数

 

 

估价函数的优化—反向传播算法（BackpropagationAlgorithm）

        对于上面的估价函数，常用的方法是利用梯度下降法来计算。在利用梯度下降法的时候，主要的两步计算是求J和在当前点的梯度。神经网络中用到了一个求梯度的非常高效的算法，即反向传播算法（BackpropagationAlgorithm）。

对于上面这个四层网络，我们可以用前向传播得到每一层每一个神经元的activation，所谓前向传播就是利用之前定义的方法，按顺序计算每层神经网络的activation，如下：

 

接下来定义每一层error的概念，用符号表示是这样

 

对于输出层的每一个神经元可以计算出它的误差

 

        因为a已经从前向传播算法中得到了，而yi就是每个样本已知的实际类别。然后计算倒数第二层的误差，当计算前面层的误差时就需要用到反向传播算法了。反向传播算法定义如下：

 

        g(z)的倒数为g(z)(1-g(z))，自己推导下，代入这个式子中。从这个式子可以看出，后一层的误差是由前一层的误差推导而来，Theta转置之后刚好和前向传播反向，这也是可以理解的。

 

 

 

这样就能通过误差，计算出每一层的delta值，而梯度就是通过该delta值来计算的。

 

然后就得到了梯度

 

 梯度校验（Gradient Checking）

 

        在实际神经网络的学习中，由于学习过程过于复杂，我们会不确定自己写的程序梯度计算对了没有，梯度校验就是一种来近似估计当前点的梯度的方法。

 

 

 

        根据导数的定义，如果elpsiton趋向于无穷小，那么约等于号右边的值正是改点的导数，于是我们就区一个非常小的elpsiton，比如elpsiton为0.001，来估计该点的梯度值。这样计算出来的梯度和实际的梯度会非常的接近。对于某一点，如果你程序计算的梯度和这样估计出来的梯度有很大的差别，那么或许是你的程序写错了。

对于每个theta就可以通过下式来求得：

 

 

另外，之所以不用梯度校验来求梯度，是因为梯度校验比反向传播算法更加复杂，计算需要消耗更多的时间，你的程序会很慢。

 

随机初始化（Random Initialization）

        如果和前面讲到的逻辑回归中的初始化一样，把全部的theta初始化为0，会出现什么问题呢？如果把所有的theta初始化一样的话，每层神经网络得到的activation也全是一样的，这样一直优化下去会得到theta值全部一样的结果，这明显对我们的模型是不利的。

解决方法就是随机初始化，先设定一个较小的值init_elpsiton，然后初始化如下

 

        这样的theta值就是在-init_elpsiton和init_elpsiton之间的随机初始值了，就可以解决上面那个问题。

另外，神经网络学习的话可以看下下面这篇文章，可以让你对神经网络由一个更好的了解。

点击打开链接