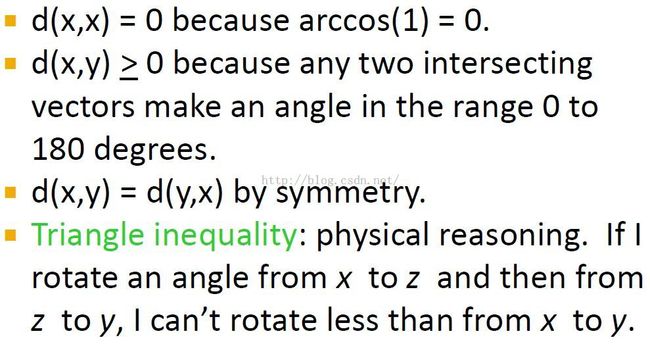海量数据挖掘MMDS week2: LSH的距离度量方法

http://blog.csdn.net/pipisorry/article/details/48882167

海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec  courses学习笔记之局部敏感哈希LSH的距离度量方法

Distance Measures距离度量方法

{There are many other notions of similarity(beyond jaccard similarity) or distance and which one to use depends on what type of data we have and what our notion of similar is.Beside it is possible to combine hash functions from a family,to get the s curve affect that we saw for LSH applied to min-hash matrices.In fact, the construction is essentially the same for any LSH family.And we'll conclude this unit by seeing some particular LSH families, and how they work for the cosine distance and Euclidean distance.}

Euclidean distance Vs. Non-Euclidean distance 欧氏距离对比非欧氏距离

Note: dense: given any two points,their average will be a point in the space.And there is no reasonable notion of the average of points in the space.欧氏距离可以计算average，但是非欧氏距离却不一定。

Axioms of Distance Measures 距离度量公理

距离度量就满足的性质

Note: iff =  if and only if [英文文献中常见拉丁字母缩写整理(红色最常见)]

皮皮blog

欧氏距离

Note: 范数Norm：
给定向量x=（x1，x2，...xn）
L1范数：向量各个元素绝对值之和，Manhattan distance。
L2范数：向量各个元素的平方求和然后求平方根，也叫欧式范数、欧氏距离。
Lp范数：向量各个元素绝对值的p次方求和然后求1/p次方
L∞范数：向量各个元素求绝对值，最大那个元素的绝对值

皮皮blog

非欧氏距离
  

Note:

1. cosine distance: requires points to be vectors, if the vectors have real numbers as components, then they are essentially points in the Euclidean space.But the vectors could have integer components in which case the space is not Euclidean.
2. 编辑距离有两种方式：一种是直接将其中一个元音字符替换成另 一个，一种是先删除字符再插入另一个字符。

非欧氏距离及其满足公理性质的证明：

Jaccard Dist

Note: Proof中使用反证法：两个都不成立，即都相等时，minhash(x)=minhash(y)了。

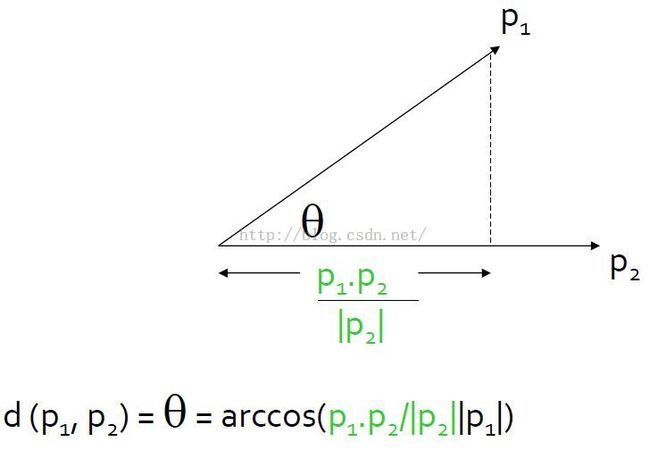
Cosine Dist余弦距离

cosine distance is useful for data that is in the form of a vector.Often the vector is in very high dimensions.

  

Note:

1. The length of a vector from the origin is actually the normal Euclidian distance,what we call the L2 norm.
2. No matter how many dimensions the vectors have, any two lines that intersect, and P1 and P2 do intersect at the origin,they'll follow a plane.
3. if you project P1 onto P2,the length of the projection is the dot product, divided by the length of P2.Then the cosine of the angle between them is the ratio of adjacent(the dot product divided by P2) over hypotenuse(斜边, the length of P1).

Note: vectors here are really directions, not magnitudes.So two vectors with the same direction and different magnitudes are really the same vector.Even to vector and its negation, the reverse of the vector,ought to be thought of as the same vector.

Edit distance编辑距离

子串的定义：one string is a sub-sequence of another if we can get the first by deleting 0 or more positions from the second.the positions of the deleted characters did not have to be consecutive.
计算x,y编辑距离的两种方式

Note: 第一种方式中我们可以逆向编辑：we can get from y to x by doing the same edits in reverse.delete u and v,and then we insert a to get x.

Hamming distance汉明距离

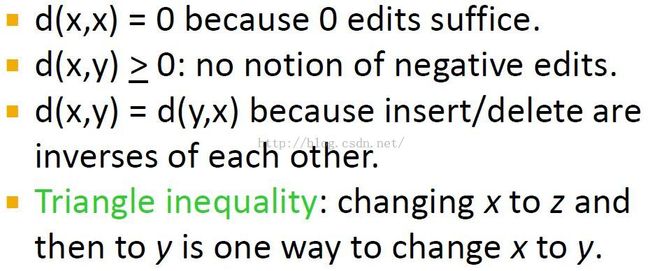
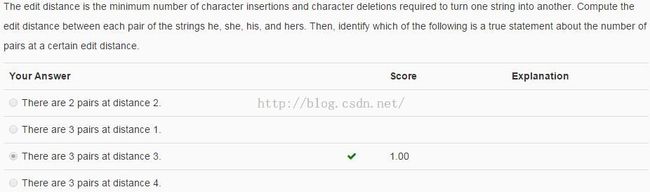
Reviews复习

Note:距离矩阵

         he     she    his    hers

he                1        3        2

she                        4        3

his                                    3

from:http://blog.csdn.net/pipisorry/article/details/48882167

ref: 距离和相似性度量方法