MIT算法导论——第二讲.Solving Recurrence
本栏目(Algorithms)下MIT算法导论专题是个人对网易公开课MIT算法导论的学习心得与笔记。所有内容均来自MIT公开课Introduction to Algorithms中Charles E. Leiserson和Erik Demaine老师的讲解。(http://v.163.com/special/opencourse/algorithms.html)
第二节-------渐近符号、递归及解法 Solving Recurrence
第二节课的内容比较偏数学化,没有算法方面的知识。但尽管如此,听着也还是比较舒服易懂。总结起来,主要有如下几个知识点。
1.渐近符号。
a、O符号。例如f(n) = O(g(n)),表示存在c > 0, n0 > 0使得0 ≤ f(n) ≤ cg(n )对于所有n ≥ n0时成立。也就是说,f(n)的复杂度最多与g(n)一个数量级,即小于等于。例如,2n^2 = O(n^3)。注意这里的等号是不对称的,只能从左到右成立反之则不成立,更形象的是记做2n^2 ∈ O(n^3)。
b、Ω符号。例如f(n) = Ω(g(n)),表示存在c > 0, n0 > 0使得0 ≤ cg(n ) ≤ f(n) 对于所有n ≥ n0时成立。也就是说,f(n)的复杂度最少与g(n)一个数量级,即大于等于。例如,n^(1/2) = Ω(lgn),应该这样理解,对于充分大的n,根号n至少是lgn的常数倍。
c、o符号。例如f(n) = o(g(n)),表示f(n)的复杂度要比g(n)的数量级小,即小于。例如,2n^2 = o(n^3),取n0 ≥ 2/c时,不等式对于所有的n0和c都是成立的。
d、ω符号。例如f(n) = ω(g(n)),表示f(n)的复杂度要比g(n)的数量级大,即大于。
e、Θ符号。例如f(n) = Θ(g(n)),表示f(n)的复杂度既大于等于g(n)的复杂度,又小于等于g(n)的复杂度,即于g(n)的复杂度相当。例如,n^2 + O(n) = Θ(n^2)。但是b中的n^(1/2) = Θ(lgn)却是不成立的,因为n的平方根的确渐近地大于lgn。我们也就不难理解n^2和n^3对于Θ也是不成立的。
2.求解递归式的方法。
一、代换法。
迄今为止还没有一个通用的方法来解递归问题,不幸的是没有一个好的算法来解递归问题。有的时候这个方法有用,有的时候这个方法凑效,如果幸运你自己的方法可以解你遇到的递归,这就有点类似于做积分。但是也跟积分一样一般来说,检查是否得到正确答案是非常容易的。这就是代换法的基本思想。
第一步:Guess the form of the solution。代换法在大多数情况下是有效的,但是不幸的是第一步需是猜答案。你不需要完全猜出来,你可以不需要知道常数系数确切是多少,仅需要猜它的形式。
第二步:通过数学归纳法验证第一步才出来的form是否满足条件。
第三步:也是第二步的必然结果,如果猜对了那么很容易解出常数系数。
例如下图所示是如何利用代换法解一个递归式:
那么,上图中证明了T(n)小于等于一个常数乘以n^3。图中所解出的答案就是上界,不过不是严格的上界,事实上我们认为n的平方也成立。所以这并不能证明递归式的答案就是n^3,这只是表示至多是O(n^3)。
二、递归树法。
递归树法是一种解递归式比较特别的方法,在第一节将归并排序的时候有用到过这个方法。它最棒的一点就是总是能用,它能告诉你一种直觉让你知道答案是多少,只是有些不严谨。所以用这个方法时要特别小心,不然可能会得到错的答案。因为它需要用到点、点、点,使用省略号来得到结论。
三、主定理方法。
主定理方法本质上可以认为是递归树方法的一个应用,但是它更精确。不同于递归树方法有省略号有待证明,主定理方法基于一个定理(主定理)。遗憾的是,主方法限制颇多只能应用到特定的递归式上。
上面的公式是在Word里面打出来后贴图上来的。接下来如下图所示,分别举出了主定理方法的三个应用场景的例子以及一个主定理方法不适用的例子。
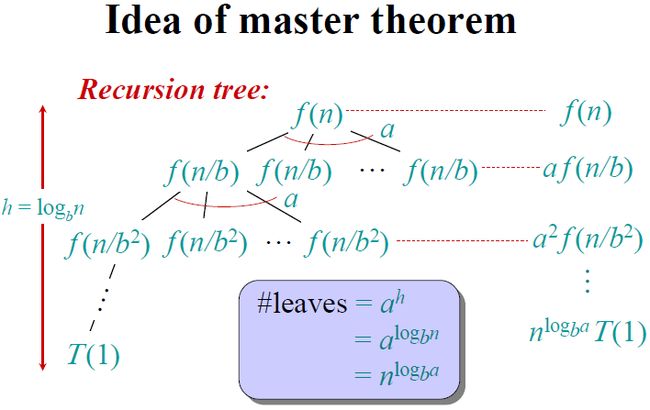
关于主定理方法的证明,下面利用递归树方法给出一个简单形象的证明。将主定理方法的递归式画成递归树如下图所示,树的高度为h,每一层效率分析如右边列出所示。其中图中紫色方框中的内容即是叶子节点效率结果的数学推导。
对于CASE 1,整个递归树的权重从根节点到叶节点一直增加,所以整个递归树的权重主要在叶子节点上;
对于CASE 2,(k = 0)递归树每层的权重大致相同,总共h层,所以整个递归树的权重将各层的权重加起来即可;
对于CASE 3,则与CASE 1的情况正好相反,所以整个递归树的权重主要在根节点上。
如上的分析,主定理方法的三种情况的结论便也不难理解。关于主定理方法的详细证明请参见CLRS。
关于Introduction to Algorithms更多的学习资料将继续更新,敬请关注本博客和新浪微博Sheridan。