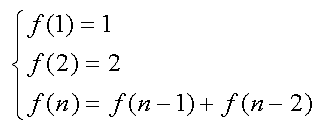走台阶问题

问题

刚才在首页看到一篇博客，说的是腾讯的一道面试题：一个楼梯有50个台阶，每一步可以走一个台阶，也可以走两个台阶，请问走完这个楼梯共有多少种方法？博主把这题分析的很麻烦。引来很多人围观。我以前也碰到过这个问题。写出来和大家分享一下。

举个例子，假设有3个台阶，则有三种走法：分别是，1-1-1, 1-2, 2-1。

分析

很简单的一道题，学过组合数学的人很快就能想到，这是一个递推关系。假设走完k个台阶有f(k)种走法。

• k = 1时，f(k) = 1
• k = 2时，f(k) = 2
• k = n时，第一步走一个台阶，剩n-1个台阶，有f(n - 1)种走法。第一步走两个台阶，剩n-2个台阶，有f(n - 2)种走法。所以共有f(n - 1) + f(n - 2)种走法。

于是有如下公式

代码

//递归算法

int count(unsigned int n)
{
    if(n == 1)
        return 1 ;
    if(n == 2)
        return 2 ;
    else 
        return count(n - 1) + count(n - 2) ;
}

//非递归算法

int count(unsigned int n)
{
 int a = 1;
 int b = 2;
 if (n == 1)
 {
 return a;
 }
 if (n == 2)
 {
 return b;
 }


 int ret = 0;
 for(int i = 2; i<n; i++)
 {
 ret = a + b;
 a = b;
 b = ret;
 }
 return b;//return ret也是可以的,看你怎么理解
}

具体是怎么走的呢？

上面只给出了有多少种走法，那么具体每一种走法是怎么走的呢？比如n=4时，五种走法分别如下：

1,1,1,1

1,1,2

1,2,1

2,1,1

2,2

我们用一个整型数组来存放每一步的内容，1表示这步走了一个台阶，2表示这步走了两个台阶。回溯法搞定。代码如下。

void count(int n, int t)
{
    if(n < 0)
        return ;
    if (n == 0)
        Output(step, t) ;
    else
    {
        for (int i = 1; i <= 2; ++i)
        {
            step[t] = i ;
            count(n - i, t + 1) ;
        }
    }
}

类似的问题

与此题类似的问题有很多，比如铺地砖问题，自然数拆分等。

铺地砖问题

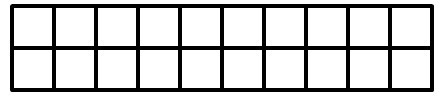
有一个长度为n,宽度为2的地面，有若干块长为2,宽为1的地砖，请问用此地砖铺完这个地面共有多少种方法？

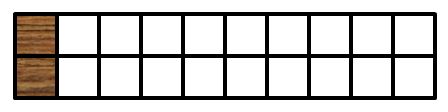
分析一下，假设铺完长度为n的地面有f(n)种方法，如果第一块地砖竖起来铺，还剩下长度为n-1的地面，有f(n-1)种方法。如下图。

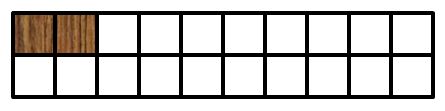
如果第一块地转横着铺，那么还剩下长度为n-2的地面，有f(n-2)种铺法(#add,横砖下面的2格也只能放个横砖,摆法已经固定)。如下图。

所以这道题与上面的题解法完全一样。不同的题目，相同的模型而已。

自然数拆分

给定一个自然数n，将其拆分为若干个自然数字之和，请问有多少种方法？举个例子，n=4时，可以拆分为1-1-1-1，1-1-2，1-3，2-2。

这题和上面的题很像，不过上面的问题是排列问题，而这题是组合问题，比如n=4时，1-1-2，1-2-1，2-1-1这三种只能算一个拆分。在上面的基础上，去掉重复的组合即可。