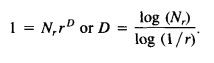fractal 分形维数 盒子维 纹理特征

分形  盒子维纹理特征

在纹理特征的提取中，纹理的分形维数特征（FD）是对纹理的一种重要描述。图像的纹理越复杂、细腻，则分形维数越大。提取分形维数特征的方法有很多种，理论以及计算的复杂度各有差异。

本文中分形维数的计算方法采用的是 DBC(Differential Box-counting)即 差分盒子计数法。该方法是由Sarkar and Chaudhuri 于1994年前后提出的(An Efficient Differential  Box-Counting Approach to Compute Fractal Dimension of  Image)，在前人的分形维数计算方法上做了重要改进，使得FD的计算以及准确度得到了较大的提升。在本文算法的编写过程中还参考了两篇中文综述：[二维灰度图像的分形维数计算.张志],[图像分形维数计算方法的比较.赵海英]。

为节省篇幅，先主要罗列所用到的基本公式，以及Sarkar原著中的论述，其他基本知识点，读者可参阅上述两篇中文综述。

 

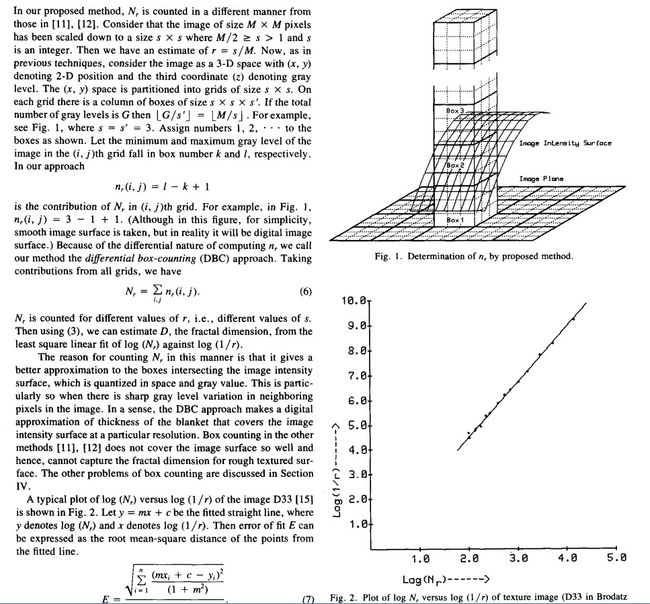
D就是要求的纹理分形维数特征。由于D是Nr、1/r对应直线的斜率，所以需要多次改变r，即网格大小，获得多个样本点，最后通过直线拟合求得最终的D。

这种基于DBC的方法计算出的纹理分形维数特征的值应该介于2~3。这是有理论证明的。在Sarkar的原著中，仅有提及，未给证明：

在[二维灰度图像的分形维数计算.张志]中作者则给出了 FD< 3 的证明。FD>2的证明类似。且在[二维灰度图像的分形维数计算.张志]中，作者提及了Sarkar的DBC方法存在的问题，即DBC方法存在多余的空盒子。所以本文在程序设计时，注意了此问题，排除了空盒子的影响，得到了较好的FD计算效果。

现给出本次设计中分形盒子维的代码。代码经验证，FD值符合纹理复杂程度。理论上，FD值本身还应具有“三不变”特性：平移、旋转、缩放。经验证，在某些图像上，本算法具备缩放不变性，平移、旋转不变形未经验证。

代码之中存在的冗余、不适、bug还望各位读者指正。

(最小二乘法拟合基本原理：http://blog.csdn.net/ice_fire3/article/details/6709929)

//************************//
//计算分形盒子维
//*** yangxin_szu 2013_03_28 ***//
//valarray与 MFC 有一定冲突 
//#undef的使用是为了避免问题出现
#ifdef min 
#undef min 
#endif 
#ifdef max 
#undef max 
#endif 
#include <valarray> 
using namespace std;
void My_Texture::Calculate_Fractal_Dim(unsigned char* Img_Data ,int Img_size)
{
	//*************************************************//
	//the width and height of the Image should be the same
	//gray level : 256
	//points for Least Square method: 20
	//*************************************************//
	int i=0 ,j=0;
	//分形盒子维相关参数
	int M = Img_size;//图像尺寸
	int G = 256;//图像灰度级
	int L_point = 20;//最小二乘法样本点数
	valarray<unsigned char> Img_VAL(Img_size*Img_size);
	valarray<int> L_VAL(L_point);
	valarray<int> h_VAL(L_point);
	valarray<double> r_VAL(L_point);
	valarray<double> Nr_VAL((double)0,L_point);
	valarray<int> Grid_Num(L_point);//网格数目
	valarray<double> fractal_D(0.0 ,L_point);
	
	//复制数据
	int k = 0;
	for (i=0;i<Img_size;i++)
	{
		for (j=0;j<Img_size;j++)
		{
			Img_VAL[k] = Img_Data[i*Img_size + j];
			k++;
		}
	}
	//网格大小及相关参数
	//改进后的约束范围 M^(1/3)<= L <= M/3
	int L_min = (int)powf(M ,1/3.0);
	//int L_min = M/40;
	int L_max = (int)M/2;
	int L_step = (int)((L_max - L_min)/(float)L_point);
	for(i=0;i<L_point;i++)
	{
		L_VAL[i] = L_min + i*L_step;//各样本点对应的网格大小     L
		h_VAL[i] = (G*L_VAL[i])/M;  //各样本点对应的盒子高度     h
		r_VAL[i] = log10(1/(L_VAL[i]/(float)M));//各样本点对应的 r
		Grid_Num[i] = M/L_VAL[i];//各样本点对应的图像网格数目    Num
	}

	int m =0,n =0,t=0;
	int grid_lt_x =0,grid_lt_y =0,grid_rd_x =0,grid_rd_y =0;
	unsigned char grid_I_max =0 ,grid_I_min =0;
	int dbc_l =0 ,dbc_k =0 ,nr =0;
	int s=0,p =0,q =0 ,box_non_zero =0,box_zero_count = 0;
	int gray_k =0,gray_l =0;
	//计算 Nr
	for (k=0;k<L_point;k++)
	{
		//临时存储单个网格数据
		valarray<unsigned char> grid_img((unsigned char)0,L_VAL[k]*L_VAL[k]);
		for (m=0;m<Grid_Num[k];m++)
		{
			for (n=0;n<Grid_Num[k];n++)
			{
				//单个网格的坐标范围
				grid_lt_x = n*L_VAL[k];
				grid_lt_y = m*L_VAL[k];
				grid_rd_x = grid_lt_x + L_VAL[k] - 1;
				grid_rd_y = grid_lt_y + L_VAL[k] - 1;
				//复制数据
				t = 0;
				for (i=grid_lt_y;i<grid_rd_y;i++)
				{
					for (j=grid_lt_x;j<grid_rd_x;j++)
					{
						grid_img[t] = Img_Data[i*M + j];
						t++;
					}
				}
				grid_I_min = grid_img.min();
				grid_I_max = grid_img.max();
				//最小、最大灰度所在的网格高度
				dbc_k = grid_I_min/h_VAL[k];
				dbc_l = grid_I_max/h_VAL[k];
				//*******计算空盒子数目********//
				for(s=dbc_k;s<=dbc_l;s++)
				{
					//灰度上下限
					gray_k = s*h_VAL[k];
				    gray_l = gray_k + h_VAL[k] - 1;
					//清零
					box_non_zero = 0;
					//落在指定盒子内的点数
					for(p=0;p<t-1;p++)
					{						
						if((grid_img[p]>=gray_k)&&(grid_img[p]<=gray_l))
							box_non_zero++;
					}
					//空盒子
					if(box_non_zero == 0)
						box_zero_count++;
				}
				//Nr累加并剔除空盒子
				nr = dbc_l - dbc_k + 1 - box_zero_count;				
				Nr_VAL[k] = Nr_VAL[k] + nr;
				//清零
				box_zero_count = 0;
			}
		}
		Nr_VAL[k] = log10(double(Nr_VAL[k]));
		grid_img.free();
	}
	//计算各样本点对应的理论斜率并保存
	fractal_D = Nr_VAL/r_VAL;
	ofstream outfile("F:\\Fractal_D.txt");//打开文件，准备写入
	for (j=0;j<L_point;j++)
	{
		outfile<<fractal_D[j]<<' '<<endl;//距离
	}
	outfile<<endl;
	outfile.close();//关闭文件，完成写入
	//****************************************//
	//最小二乘法拟合直线
	double A = 0.0;
	double B = 0.0;
	double C = 0.0;
	double D = 0.0;

	A = (r_VAL*r_VAL).sum();
	B = r_VAL.sum();
	C = (r_VAL*Nr_VAL).sum();
	D = Nr_VAL.sum();

	double fractal_k,fractal_b,tmp =0;
	if(tmp=(A*L_point-B*B))
	{
		fractal_k = (C*L_point-B*D)/tmp;
		fractal_b = (A*D-C*B)/tmp;
	}
	else
	{
		fractal_k = 1;
		fractal_b = 0;
	}
	//拟合得到的分形盒子维
	m_fractal_dim = fractal_k;
	m_fractal_shift = fractal_b;

	//释放所有 valarray对象
	Img_VAL.free();
	L_VAL.free();
	h_VAL.free();
	r_VAL.free();
	Nr_VAL.free();
	Grid_Num.free();
	fractal_D.free();

}

算法效果：

  

FD = 2.73                           FD = 2.85

FD = 2.14                           FD = 2.16                     FD = 2.886

上图中黑色图像可能由于制图时截图所致，边缘像素以及图像品质变化，图像并非纯黑，且FD是由点拟合而来，所以此时的FD没能等于 2.由以上5幅图像可见，FD与纹理分布的细密、复杂程度符合得较好。