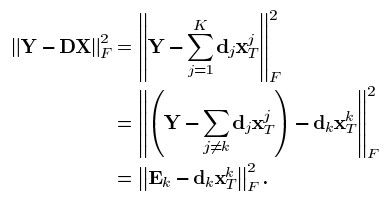K-SVD算法
1、目标：找到一个字典D，使得对于给定的训练信号集能获得稀疏表达。具体目标为：
2、具体迭代步骤
（1）第一阶段：固定字典 D ，找最好的稀疏矩阵 X 。
此为NP难问题。 给定T0，可以采用任何approximation pursuit method去求解 X。论文采用OrthogonalMatching Pursuit (OMP) algorithms。
（2）第二阶段：也是K-SVD与MOD的不同之处，字典D是逐列更新的。
假设系数X和字典D都是固定的，要更新字典的第k列dk，令稀疏矩阵X中与dk相乘的第k行记做，则目标函数可以重写为：
上式中，DX被分解为K个秩为1的矩阵的和，假设其中K-1项都是固定的，剩下的1列就是要处理更新的第k个。矩阵Ek表示去掉原子dk的成分在所有N个样本中造成的误差。
如果在这一步就用SVD更新dk和，SVD能找到距离Ek最近的秩为1的矩阵，但这样得到的系数
不稀疏，换句话说，
与更新dk前的非零元所处位置和value不一样。那怎么办呢？直观地想，只保留系数中的非零值，再进行SVD分解就不会出现这种现象了。所以对Ek和
做变换，
中只保留x中非零位置的，Ek只保留dk和
中非零位置乘积后的那些项。形成，将
SVD分解，更新dk。
3、K-SVD总可以保证误差单调下降或不变，但需要合理设置字典大小和稀疏度。
4、在Michael Elad的主页上有KSVD的matlab代码下载：http://www.cs.technion.ac.il/~elad/software/。感觉速度还是有点慢。
A newer version with various improvements, created by Ron Rubinstein, is available in his webpag:
http://www.cs.technion.ac.il/~ronrubin/software.html
参考文献：
1、Michal Aharon Michael Elad Alfred Bruckstein Yana Katz，K-SVD: An Algorithm for Designing of Overcomplete Dictionaries for Sparse Representation，IEEE Transactions on Signal Process, vol. 54, no. 11, 2006
2、Rachel Zhang的博客：http://blog.csdn.net/abcjennifer/article/details/8693342