kmp算法

最近在复习算法方面的知识，看到了KMP，大学里面数据结构和算法，老师让买的全英文的教材，估计那会儿精力全在翻译英文去了，这个算法完全没有掌握。

下面的链接是综合了两个同学的链接，再加上我自己对关键地方的注释（红色字体部分）。

http://www.cnblogs.com/yjiyjige/p/3263858.html

http://billhoo.blog.51cto.com/2337751/411486 

【KMP算法简介】

 

         KMP算法是一种改进后的字符串匹配算法，由D.E.Knuth与V.R.Pratt和J.H.Morris同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法）。通过一个辅助函数实现跳过扫描不必要的目标串字符，以达到优化效果。

 

 

 

【传统字符串匹配算法的缺憾】

 

         Bill认为，对于一种优化的算法，既要知道优化的细节，也更应该了解它的前身（至于KMP是否基于传统算法，我不清楚，这里只作语境上的前身），了解是什么原因导致了人们要去优化它，因此加入了这一段：

请看以下传统字符串匹配的代码：

C++ code

 

void NativeStrMatching( ElemType Target[], ElemType Pattern[] )            
{            
        register int TarLen = 0;        // Length of Target            
        register int PatLen = 0;        // Length of Pattern            
         
        // Compute the length of Pattern            
        while( '\0' != Pattern[PatLen] )            
                PatLen++;            
         
        while( '\0' != Target[TarLen] )            
        {            
                int TmpTarLen = TarLen;            
                for(int i=0; i<PatLen; i++)            
                {            
                        if( Target[TmpTarLen++] != Pattern[i] )            
                                break;            
                        if( i == PatLen-1 )            
                                cout<<"Native String Matching,pattern occurs with shift "<<TarLen<<endl;            
                }            
                TarLen++;            
        }            
}    

 

【代码思想】

     传统匹配思想是，从目标串Target的第一个字符开始扫描，逐一与模式串的对应字符进行匹配，若该组字符匹配，则检测下一组字符，如遇失配，则退回到Target的第二个字符，重复上述步骤，直到整个Pattern在Target中找到匹配，或者已经扫描完整个目标串也没能够完成匹配为止。

     这样的算法理解起来很简单，实现起来也容易，但是其中包含了过多不必要的操作，也就是在目标串中，有些字符是可以直接跳过，不必检测的。

不妨假设我们的目标串

Target =  "a b c d e a b c d e a b c d f"

需要匹配的模式串

Pattern = "c d f";

那么当匹配到如下情况时

 

       

 

 

 

由于 'e' != 'f' ，因此失配，那么下次匹配起始位置就是目标串的'd'字符

     

 

 

 

 

 

我们发现这里照样失配，直到运行到下述情况

 

 

 

 

 

 

 

也就是说，中间的四个字符 d e a b 完全没有必要检测，直接跳转到下一个'c'开始的地方进行检测  

    

     由此可见传统算法虽然简单易行，但其中包含了过多的不必要操作，并不能很好地达到实际工作中需要的效率，因此个人认为此方法适合为初识字符串匹配做一个铺垫作用，有抛砖引玉之意。

     说其抛砖引玉并不为过，对KMP算法的理解便可以基于传统模式串匹配算法进行思考。

 

 

 

【KMP算法的引入】

 

     既然知道了传统算法的不足之处，就要对症下药，优化这个冗余的检测算法。

     KMP算法就能很好地解决这个冗余问题。

     其主要思想为：

          在失配后，并不简单地从目标串下一个字符开始新一轮的检测，而是依据在检测之前得到的有用信息（稍后详述），直接跳过不必要的检测，从而达到一个较高的检测效率。

     如我们的

 

 

        当第一次失配后，并不从红色标记字符'd'开始检测，而是通过一些有用信息，直接跳过后几个肯定不可能匹配的冗余字符，而直接让模式串Pattern从目标串的红色标记字符'c'开始新一轮的检测，从而达到了减少循环次数的效果

 

 

 

【KMP算法思想详述与实现】

 

        前面提到，KMP算法通过一个“有用信息”可以知道目标串中下一个字符是否有必要被检测，这个“有用信息”就是用所谓的“前缀函数（一般数据结构书中的next函数）”来存储的。

        这个函数能够反映出现失配情况时，系统应该跳过多少无用字符（也即模式串应该向右滑动多长距离）而进行下一次检测，在上例中，这个距离为4.

        总的来讲，KMP算法有2个难点：

              一是这个前缀函数的求法。

              二是在得到前缀函数之后，怎么运用这个函数所反映的有效信息避免不必要的检测。

下面分为两个板块分别详述：

 

 

【前缀函数的引入及实现】

 

【前缀函数的引入】

        对于前缀函数，先要理解前缀是什么：

        简单地说，如字符串A = "abcde"        B = "ab"

        那么就称字符串B为A的前缀，记为B ⊏ A(注意那不是"包含于"，Bill把它读作B前缀于A)，说句题外话——"⊏"这个符号很形象嘛，封了口的这面相当于头，在头前面的就是前缀了。

        同理可知 C = "e","de" 等都是 A 的后缀，以为C ⊐ A（Bill把它读作C后缀于A）

       A 的前缀有 a，ab，abc，abcd，abcde。A的的真前缀是 a，ab，abc，abcd。即真前缀是前缀中去除本身。    

       A 的后缀有 e，de，cde，bcde，abcde。A的的真后缀是  e，de，cde，bcde。即真后缀是后缀中去除本身。    

      

理解了什么是前、后缀，就来看看什么是前缀函数：

        在这里不打算引用过多的理论来说明，直接引入实例会比较容易理解，看如下示例：

 

      (下述字符若带下标，则对应于图中画圈字符)

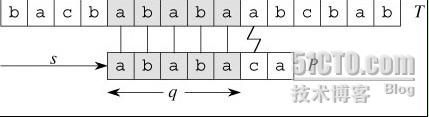
      这里模式串 P = “ababaca”,在匹配了 q=5 个字符后失配，因此，下一步就是要考虑将P向右移多少位进行新的一轮匹配检测。传统模式中，直接将P右移1位，也就是将P的首字符'a'去和目标串的'b'字符进行检测，这明显是多余的。通过我们肉眼的观察，可以很简单的知道应该将模式串P右移到下图'a3'处再开始新一轮的检测，直接跳过肯定不匹配的字符'b'，那么我们“肉眼”观察的这一结果怎么把它用语言表示出来呢？

 

     我们的观察过程是这样的：

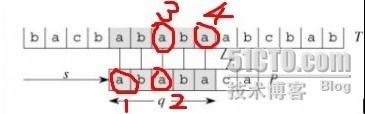
          P的前缀"ab"中'a' != 'b'，又因该前缀已经匹配了T中对应的"ab"，因此，该前缀的字符'a1'肯定不会和T中对应的字串"ab"中的'b'匹配，也就是将P向右滑动一个位移是无意义的。

          接下来考察P的前缀"aba"，发现该前缀自身的前缀'a1'与自身后缀'a2'相等，"a1 b a2" 已经匹配了T中的"a b a3"，因此有 'a2' == 'a3', 故得到 'a1' == 'a3'......

          利用此思想，可推知在已经匹配 q=5 个字符的情况下，将P向右移 当且仅当 2个位移时，才能满足既没有冗余(如把'a'去和'b'比较)，又不会丢失(如把'a1' 直接与 'a4' 开始比较，则丢失了与'a3'的比较)。

          而前缀函数就是这样一种函数，它决定了q与位移的一一对应关系，通过它就可以间接地求得位移s。

   

     通过对各种模式串进行上述分析(大家可以自己多写几个模式串出来自己分析理解)，发现给定一个匹配字符数 q ，则唯一对应一个有效位移，如上述q=5,则对应位移为2.

     这就形成了一一对应关系，而这种唯一的关系就是由前缀函数决定的。

     这到底是怎样的一种关系呢？

     通过对诸多模式串实例的研究，我们会找到一个规律（规律的证明及引理详见《算法导论(第二版)》）。

     上例中，P 已经匹配的字符串为"ababa",那么这个字符串中，满足既是自身真后缀(即不等于自身的后缀)，又是自身最长前缀的字符串为"aba"，我们设这个特殊字串的长度为L，显然，L = 3. 故我们要求的 s = q - L = 5 - 3 = 2 ，满足前述分析。

   

     根据这个规律，即可得到我们要求的有效位移s，等于已经匹配的字符数 q 减去长度 L。

     即 s = q - L

     因为这个长度 L 与 q 一一对应，决定于q，因此用一函数来表达这一关系非常恰当，这就是所谓的前缀函数了。

     因为已经分析得到该关系为一一对应关系，因此用数组来表示该函数是比较恰当的，以数组的下标表示已经匹配的字符数 q，以下标对应的数据存储 L。

      所以前缀函数就是求有n个字符匹配时，这n个字符的 最长真后缀同时又是前缀的字符串的长度。

 

【前缀函数的实现】

   

下面就来分析怎么用代码来表达这种关系。

这里采用《算法导论(第二版)》中的思想求解。

不妨以 PrefixFunc[] 表示这个前缀函数，那么我们将得到以下求前缀函数的函数：

由于 0 个匹配字符数在计算中没有意义，因此PrefixFunc下标从1开始，也就是从已经有一个字符(即首字符)匹配的情况开始

C++ code

 

// Compute Prefix function            
void CptPfFunc( ElemType Pattern[], int PrefixFunc[] )                
{      

        int iLen = 0;    // Length of Pattern[]            
        while( '\0' != Pattern[iLen] )            
                iLen++;            
                    
        int LOLP = 0;     // Lenth of longest prefix            
        PrefixFunc[1] = 0;            
         

         // NOCM represent the count of characters matched
        for( int NOCM=2; NOCM<iLen+1; NOCM++ ) 
        {            
                while( LOLP>0 && (Pattern[LOLP] != Pattern[NOCM-1]) )            
                        LOLP = PrefixFunc[LOLP];            
                if( Pattern[LOLP] == Pattern[NOCM-1] )            
                        LOLP++;            
                PrefixFunc[NOCM] = LOLP;            
        }            
}            
    

  现在分析一下这段代码的意思，

while( LOLP>0 && (Pattern[LOLP] != Pattern[NOCM-1]) )            
                        LOLP = PrefixFunc[LOLP];

情况一：    

上一步 x1，x2

当前步x1，x2，x3，因为上一步中x1不等于x2，所以LOLP == 0；

所以，while直接跳过。

情况二:

上一步x1，x2，x3，x1，x2

当前步x1，x2，x3，x1，x2，x3

由于上一步有最长真前缀同时又是后缀 x1，x2，所以LOLP为2，此时Pattern[LOLP]  != Pattern[NOCM-1] 就是比较上一步最长真前缀的下一个字符于当前步新添加的字符是否相等。如果相等的话，那么最长真前缀就加1。具体逻辑是While判断依然直接跳过。执行后面的If判断，此时If必定为真，所以LOLP++;

情况三：

上一步 x1，x2，x1 ，x3， x1，x2，x1

当前步x1，x2，x1，x3，x1，x2，x1，x2

同理上一步有最长真前缀同时又是后缀， x1，x2，x1， 此时LOLP为3，同理判断 Pattern[LOLP]  != Pattern[NOCM-1] ，此时不等。

但是由于在此之前是有最长真前缀的，所以，(上一步的前缀)的前缀部分与(上一步的后缀)的后缀部分是相等的。

上一步的前缀 x1，x2，x1， 它的前缀部分 x1

上一步的后缀x1，x2，x1，它的后缀部分x1

因此需要接着判断由上一步的前缀的和前缀后一个字符组合起来，与上一步的后缀和当前步加起来的字符是否相等。

即我们判断完

( x1，x2，x1， x3)    ( x1，x2，x1，x2)

之后还需要判断这个组合是否相等

(x1，x2)，x1，x3     x1，x2，(x1，x2)

所以将LOLP = PrefixFunc[LOLP];   即是求出（上一步的最长前缀）的最长前缀值。

通过while一直递归到上一步的前缀没有前缀为止。

 对此函数的详解，不妨以一实例带入(建议大家自己手算一下，算完应该就有感觉了)，易于理解：

                            

 不妨设模式串Pattern = "a  b  c  c  a  b  c  c  a  b  c  a"

      Pattern 数组编号： 0  1  2  3  4  5  6  7  8  9 10 11

NOCM 表示 已经匹配的字符数

LOLP 表示 既是自身真后缀又是自身最长前缀的字符串长度

以下是计算流程：

PrefixFunc[1] = 0； //只匹配一个字符就失配时，显然该值为零

LOLP = 0；   NOCM = 2；   LOLP = 0;    PrefixFunc[2] = 0;

LOLP = 0；   NOCM = 3；   LOLP = 0;    PrefixFunc[3] = 0;

LOLP = 0；   NOCM = 4；   LOLP = 0;    PrefixFunc[4] = 0;

LOLP = 0；   NOCM = 5；   LOLP = 1;    PrefixFunc[5] = 1;

LOLP = 1；   NOCM = 6；   LOLP = 2;    PrefixFunc[6] = 2;

LOLP = 2；   NOCM = 7；   LOLP = 3;    PrefixFunc[7] = 3;

LOLP = 3；   NOCM = 8；   LOLP = 4;    PrefixFunc[8] = 4;

LOLP = 4；   NOCM = 9；   LOLP = 5;    PrefixFunc[9] = 5;

LOLP = 5；   NOCM = 10； LOLP = 6;    PrefixFunc[10] = 6;

LOLP = 6；   NOCM = 11； LOLP = 7;    PrefixFunc[11] = 7;

LOLP = 7；   NOCM = 12；

---------此时满足条件while( LOLP>0 && (Pattern[LOLP] != Pattern[NOCM-1]) )-------------

while语句中的执行

{

           LOLP = 7;   NOCM = 12;  LOLP = PrefixFunc[7] = 3;

           LOLP = 3;   NOCM = 12;  LOLP = PrefixFunc[3] = 0;

}

LOLP = 0；   NOCM = 12； LOLP = 1;    PrefixFunc[12] = 1;

最后我们的前缀函数 PrefixFunc[] = { 0,0,0,0,1,2,3,4,5,6,7,1 }

其间最精妙的要属失配时的操作

while( LOLP>0 && (Pattern[LOLP] != Pattern[NOCM-1]) )
              LOLP = PrefixFunc[LOLP];

其中 LOLP = PrefixFunc[LOLP];  递归调用PrefixFunc函数，直到整个P字串都再无最长前缀或者找到一个之前的满足条件的最长前缀。

 

 

 

 

  【应用前缀函数优化传统匹配算法——KMP算法实现】

由以上分析，不难推导KMP算法的实现

C++ code

void KMPstrMatching( ElemType Target[], ElemType Pattern[] )            
{            
        int PrefixFunc[MAX_SIZE];            
        register int TarLen = 0;            
        register int PatLen = 0;            
         
        // Compute the length of array Target and Pattern            
        while( '\0' != Target[TarLen] )            
                TarLen++;            
         
        while( '\0' != Pattern[PatLen] )            
                PatLen++;            
                    
        // Compute the prefix function of Pattern            
        CptPfFunc( Pattern, PrefixFunc );            
         
        int NOCM = 0;     // Number of characters matched            
         
        for( int i=0; i<TarLen; i++ )            
        {            
                while( NOCM>0 && Pattern[NOCM] != Target[i] )            
                        NOCM = PrefixFunc[NOCM];            
                if( Pattern[NOCM] == Target[i] )            
                        NOCM++;            
                if( NOCM == PatLen )            
                {            
                        cout<<"KMP String Matching,pattern occurs with shift "<<i - PatLen + 1<<endl;            
                        NOCM = PrefixFunc[NOCM];            
                }            
        }            
}        

我的注释：

注意，这里又有点意思了，这个算法分析出当字符不匹配的时候，是保持主链上的指针不动，然后将匹配链的指针移动。

本来上面分析的是，如果不匹配，就将主链指针移动到我们上面算出来的值，然后将匹配链指针重新置到头部，比如：

其中

红色位主链指针当前位置

蓝色位匹配链指针当前位置

主链：     x1，x2，x3， x1，x2， x4，x5，x6

匹配链： x1，x2，x3， x1，x2， x7

按照上面的分析调整后应该是归置到这样的：

主链：     x1，x2，x3， x1 ，x2，x4 ，x5，x6

匹配链：                           x1 ，x2，x3，x1，x2， x7

但是我们经过分析发现，主指针往前移动的部分是完全不需要比较的，比如上例中的x1，x2。

为什么，因为我们移动实际上是讲主链移动了上一步的最长真后缀长度，而匹配连是移动到了开头，而从开头起的最长真前缀长度的字符和主链上最长真后缀是一样的，下图中蓝色部分：

主链：     x1，x2，x3， x1，x2 ， x4 ，x5，x6

匹配链： x1，x2 ，x3，x1，x2， x7

所以实际有必要的比较还是从主链当前的位置开始比较，所以改进的方式就是主链不动，只移动匹配链，如图：

主链：     x1，x2，x3， x1，x2， x4 ，x5，x6

匹配链：                          x1，x2， x3 ，x1，x2，x7

这就是为什么下面这个while循环的来历：

说明一下，由于PrefixFunc是按1开始有效的，而Pattern是按0开始计算的。比如NOCM等于5，那么Pattern[5]实际上是第6个字符。而PrefixFunc[5]是有5个字符串时的最长真前缀的长度。

 for( int i=0; i<TarLen; i++ )            
        {            
                while( NOCM>0 && Pattern[NOCM] != Target[i] )            
                        NOCM = PrefixFunc[NOCM];            
                if( Pattern[NOCM] == Target[i] )            
                        NOCM++;            
                if( NOCM == PatLen )            
                {            
                        cout<<"KMP String Matching,pattern occurs with shift "<<i - PatLen + 1<<endl;            
                        NOCM = PrefixFunc[NOCM];            
                }            
        }