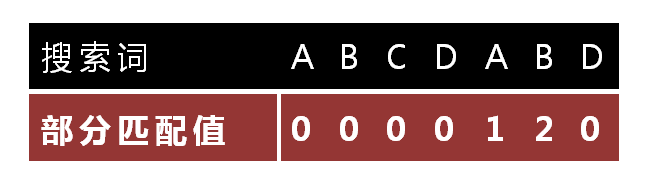KMP算法
转自:http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
http://www.geeksforgeeks.org/searching-for-patterns-set-2-kmp-algorithm/
1.
首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。
2.
因为B与A不匹配,搜索词再往后移。
3.
就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
4.
接着比较字符串和搜索词的下一个字符,还是相同。
5.
直到字符串有一个字符,与搜索词对应的字符不相同为止。
6.
这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
7.
一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
8.
怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。
9.
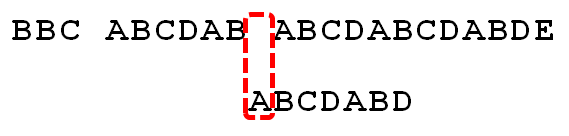
已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。
10.
因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
11.
因为空格与A不匹配,继续后移一位。
12.
逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
13.
逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
14.
下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
15.
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
16.
"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
void computeLPSArray(char *pat, int M, int *lps);
void KMPSearch(char *pat, char *txt)
{
int M = strlen(pat);
int N = strlen(txt);
// create lps[] that will hold the longest prefix suffix values for pattern
int *lps = (int *)malloc(sizeof(int)*M);
// Preprocess the pattern (calculate lps[] array)
computeLPSArray(pat, M, lps);
int i = 0; // index for txt[]
int j = 0; // index for pat[]
while(i < N)
{
if(pat[j] == txt[i])
{
j++;
i++;
}
if (j == M)
{
printf("Found pattern at index %d \n", i-j);
j = lps[j-1];
}
else if(pat[j] != txt[i])
{
// Do not match lps[0..lps[j-1]] characters,
// they will match anyway
if(j != 0)
j = lps[j-1];
else
i = i+1;
}
}
free(lps); // to avoid memory leak
}
void computeLPSArray(char *pat, int M, int *lps)
{
int len = 0; // lenght of the previous longest prefix suffix
lps[0] = 0; // lps[0] is always 0
int i = 1;
// the loop calculates lps[i] for i = 1 to M-1
while(i < M)
{
if(pat[i] == pat[len])
{
len++;
lps[i] = len;
i++;
}
else // (pat[i] != pat[len])
{
if( len != 0 )
{
// This is tricky. Consider the example AAACAAAA and i = 7.
len = lps[len-1];
// Also, note that we do not increment i here
}
else // if (len == 0)
{
lps[i] = 0;
i++;
}
}
}
}
// Driver program to test above function
int main()
{
char *txt = "ABABDABACDABABCABAB";
char *pat = "ABABCABAB";
KMPSearch(pat, txt);
getchar();
return 0;
}