CodeForces 444C. DZY Loves Physics（枚举+水题）

转载请注明出处：http://blog.csdn.net/u012860063/article/details/37509207

题目链接：http://codeforces.com/contest/445/problem/C

----------------------------------------------------------------------------------------------------------------------------------------------------------

欢迎光临天资小屋：http://user.qzone.qq.com/593830943/main

----------------------------------------------------------------------------------------------------------------------------------------------------------

DZY Loves Physics

DZY loves Physics, and he enjoys calculating density.

Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:

where  v is the sum of the values of the nodes,  e is the sum of the values of the edges.

Once DZY got a graph G, now he wants to find a connected induced subgraph G' of the graph, such that the density of G' is as large as possible.

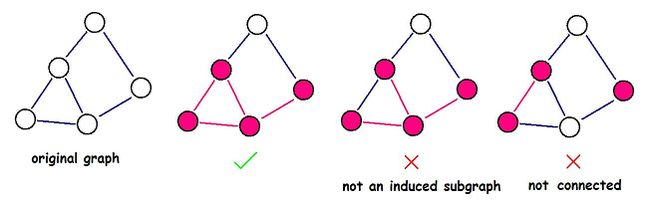
An induced subgraph G'(V', E') of a graph G(V, E) is a graph that satisfies:

• ;
• edge  if and only if , and edge ;
• the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node.

Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.

Input

The first line contains two space-separated integers n (1 ≤ n ≤ 500), . Integer n represents the number of nodes of the graph G, m represents the number of edges.

The second line contains n space-separated integers xi (1 ≤ xi ≤ 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.

Each of the next m lines contains three space-separated integers ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103), denoting an edge between node ai and bi with value ci. The graph won't contain multiple edges.

Output

Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.

Sample test(s)

input

1 0
1

output

0.000000000000000

input

2 1
1 2
1 2 1

output

3.000000000000000

input

5 6
13 56 73 98 17
1 2 56
1 3 29
1 4 42
2 3 95
2 4 88
3 4 63

output

2.965517241379311

Note

In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.

In the second sample, choosing the whole graph is optimal.

题意：   给出一个源图， 要求寻找一个密度（点的值/边的值）最大的子图；

当然子图有三个要满足的要求！

思路：枚举每天边，及其端点的值。为什么这就是最大密度的子图呢？

因为子图必然是由很多边和端点所组成的，而想要最大密度的子图，必然子图中其中的一条边的密度是最大的（至少不会小于子图的总密度），这样只需要找出密度最大的边就是答案.

代码如下：

#include <cstdio>
#define N 517
double MAX(double a, double b)
{
	return a>b?a:b;
}
int main()
{
	int n, m;
	int x[N];
	int a, b, c;
	while(~scanf("%d%d",&n,&m))
	{
		int i, j;
		for(i = 1; i <= n; i++)
		{
			scanf("%d",&x[i]);
		}
		double max = 0, t;
		for(i = 1; i <= m; i++)
		{
			scanf("%d%d%d",&a,&b,&c);
			t =(double) (x[a]+x[b])/c;
			max = MAX(max, t);
		}
		printf("%.15f\n",max);
	}
	return 0;
}