一元线性回归分析

最小二乘法求直线回归方程

假定已经给离散点配置了一条直线y'=a+bx,则y'i是相应于xi的回归直线的理论值,而yi则是相应于xi的测试值.测称vi=yi-y'i为回归直线的残差,vi实际上就是yi这一点相对于回归直线的误差.这样把求最佳值的原理用于求解回归直线方程,就能得到最佳配置的直线.

求解最佳回归方程的原则是:由这条直线的方程与全部测定值所计算的残差平方和为最小,即:

若有N对测定值(xi,yi),i=1,2,....N,则可以列出N个残差方程.将每个方程的两边取平方,然后左右两边分别取总和,即得到求解的最佳回归方程的条件,从概率分布的角度来说,直线上个点出现的概率是最大的,这些嗲所代表的数值即为回归的最佳值或最可信赖值.

为了满足上式的条件,根据微分学的知识知道,必须使上式左边对a和b的偏微分分别为0,即:,微分后得到,求解可得:,a、b即为最佳回归直线的系数.在求出系数b后,系数a的值可以推到如下:.对b值的计算公式进一步推演可得.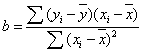

相关系数

在用上述方法求解回归方程的过程中,实际上并不需要事先假定两个变量之间具有相关关系,也就是说,可以不加任何条件作为约束就能进行这种运算,即使散点图杂乱分布也总能给他配上一条直线.显然在这种情况下所配的直线是毫无意义的,因此,我们需要一个衡量变量之间相关关系的标准.为此,引入相关系数.

首先看回归系数b,b是方程中的斜率,其他大小决定y随x变化的程度,如果y与x没有相关关系,即零相关,此时y将不随x的变化而变化,b应为零,y就是一天直线.于是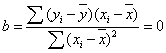,如果反过来把y看成自变量,x作为因变量,则可得到这种情况下的回归方程:x=a'+b'y.可得到,由于相关关系是相互的,既然x不随y变化,y也不随x变化,则b'=0,此时可以得到x和y不相关时的一种情况,相反,如果x与y全相关,即所有观测值的点都通过回归直线,显然y=a+bx与x'=a'+b'y代表着同一天直线,直线斜率b和b'的关系互为倒数,由此得到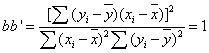,他的数值代表了两个变量之间相关的紧密程度,因此吧这个式子的平方根定义为相关系数r,即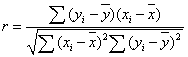

根据前面所述可知r的性质如下:

1.由于r与b值b'值得数学式中的分子相同,而他们的分明由于是平方项,因而肯定为非零的正值,故当r=0时,b=0且有b'=0，x和y毫无线性相关关系.

2.当0<|r|<1时,y与x存在一定的线性相关关系,当r>0时,b和b'均大于零,即y有随x的增大而增大的趋势,次即正相关,当r<0时,b或b'小于零,次即负相关,|r|值越大,相关关系越紧密,散点图的分布越集中,趋势越明显,反之亦然.

3.|r|=1时,所有的点都落在回归直线上,即完全线性相关,其中r=1为完全正相关,r=-1为完全负相关.

4.相关系数与回归系数的关系为r=sqrt(b*b'),所以r值介于两个回归系数之间,是他们的几何平均值.

剩余标准误差: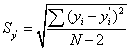yi为实测值,yi'为回归直线的理论值,(yi-yi')又称回归直线的余差.N-2为自由度.

剩余平方和:

一元线性回归的实现:

//n观测点的个数
void LinearRegression(double *x,double *y,int n)
{
	double xsum=0;
	double xave=0;
	double ysum=0;
	double yave=0;
	double *yhat=(double*)malloc(sizeof(double)*n);
	//yhat:y的估计值
	double a,b,r;
	//a,b,直线系数,r相关系数
	double lyy,U,Q,Sy,Sq,Syhat,Sa,Sb;
	//lyy:总平方和
	//U:回归平方和
	//Q:剩余平方和
	//Sy:总均方差
	//Sq:回归均方差
	//Syhat:剩余均方差
	//Sa:a的均方差
	//Sb:b的均方差
	double deltayy,y1,y2;
	//deltayy:回归直线的误差
	//y1,y2:回归直线误差的上下限
	for(int i=0;i<n;i++)
	{
		xsum+=x[i];
		ysum+=y[i];
	}
	xave=xsum/n;
	yave=ysum/n;
	
	double sum1=0,sum2=0;
	for(int i=0;i<n;i++)
	{
		sum1+=(y[i]-yave)*(x[i]-xave);
		sum2+=(x[i]-xave)*(x[i]-xave);
	}
	b=sum1/sum2;				//求系数a
	a=yave-b*xave;				//求系数b

	double sum3=0;
	for(int i=0;i<n;i++)
	{
		sum3+=(y[i]-yave)*(y[i]-yave);
	}
	r=sum1/sqrt(sum2*sum3);		//相关系数

	for(int i=0;i<n;i++)
	{
		yhat[i]=a+b*x[i];
	}
	
	lyy=sum3;					//总平方和
	//
	U=0;						//回归平方和
	for(int i=0;i<n;i++)
	{
		U+=(yhat[i]-yave)*(yhat[i]-yave);
	}
	Q=lyy-U;					//剩余平方和

	Sy=sqrt(lyy/(n-1));				//总均方差
	Sq=sqrt(Q);					//回归均方差
	Syhat=sqrt(U/(n-2));				//剩余均方差

	Sa=Syhat*sqrt(1/n+xave*xave/sum2);		//a的均方差
	Sb=Syhat/sqrt(sum2);				//b的均方差
	//deltayy=Syhat*sqrt(1+1/n+sum2/)

	printf("直线方程为:y=%lf+%lf*x\n相关系数r=%lf\n",a,b,r);
	printf("总平方和:%lf\t总均方差%lf\n",lyy,Sy);
	printf("回归平方和:%lf\t回归均方差%lf\n",U,Sq);
	printf("剩余平方和:%lf\t剩余均方差%lf\n",Q,Syhat);
	printf("a的均方差:%lf\tb的均方差:%lf\n",Sa,Sb);
	printf("实测值:\t估计值:\t差值:\n");
	for(int i=0;i<n;i++)
	{
		printf("%.02lf\t%0.2lf\t%0.2lf\n",y[i],yhat[i],y[i]-yhat[i]);
	}
	free(yhat);
}