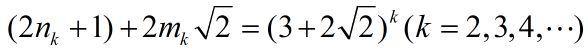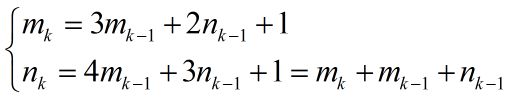UVa 138 Street Numbers(数论&Pell方程)

138 - Street Numbers

Time limit: 3.000 seconds

http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=115&page=show_problem&problem=74

A computer programmer lives in a street with houses numbered consecutively (from 1) down one side of the street. Every evening she walks her dog by leaving her house and randomly turning left or right and walking to the end of the street and back. One night she adds up the street numbers of the houses she passes (excluding her own). The next time she walks the other way she repeats this and finds, to her astonishment, that the two sums are the same. Although this is determined in part by her house number and in part by the number of houses in the street, she nevertheless feels that this is a desirable property for her house to have and decides that all her subsequent houses should exhibit it.

Write a program to find pairs of numbers that satisfy this condition. To start your list the first two pairs are: (house number, last number):

         6         8
        35        49

Input and Output

There is no input for this program. Output will consist of 10 lines each containing a pair of numbers, each printed right justified in a field of width 10 (as shown above).

记房子数为n，程序猿住在m号房（m<n），简单推导一下有2m^2=n(n+1)

整理得n^2-2m^2+n=0

配方，转化为Pell方程：(2n+1)^2-2(2m)^2=1

参考《数论概论》P230-231有

即

展开得到递推公式：

解得以下前10组数据

6, 8

35, 49

204, 288

1189, 1681

6930, 9800

40391, 57121

235416, 332928

1372105, 1940449

7997214, 11309768

46611179, 65918161

完整代码：（注意输出格式~）

/*0.012s*/

#include<cstdio>
using namespace std;

int main()
{
	int t = 10, m = 1, n = 1, temp;
	while (t--)
	{
		temp = 3 * m + 2 * n + 1;
		n += temp + m;
		m = temp;
		printf("%10d%10d\n", m, n);
	}
	return 0;
}

打表：

/*0.009s*/

#include <cstdio>
using namespace std;

int main()
{
    printf("%10d%10d\n", 6, 8);
    printf("%10d%10d\n", 35, 49);
    printf("%10d%10d\n", 204, 288);
    printf("%10d%10d\n", 1189, 1681);
    printf("%10d%10d\n", 6930, 9800);
    printf("%10d%10d\n", 40391, 57121);
    printf("%10d%10d\n", 235416, 332928);
    printf("%10d%10d\n", 1372105, 1940449);
    printf("%10d%10d\n", 7997214, 11309768);
    printf("%10d%10d\n", 46611179, 65918161);
    return 0;
}