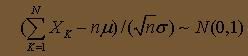随机函数的底层深入探究
原文链接
摘要:
本文简述了随机数的产生原理,并用C语言实现了迭代取中法,乘同余法等随机数产生方法,同时,还给出了在符合某种概率分布的随机变量的产生方法。
关键词: 伪随机数产生,概率分布
1前言:
在用计算机编制程序时,经常需要用到随机数,尤其在仿真等领域,更对随机数的产生提出了较高的要求,仅仅使用C语言类库中的随机函数已难以胜任相应的工作。本文简单的介绍随机数产生的原理及符合某种分布下的随机变量的产生,并用C语言加以了实现。当然,在这里用计算机基于数学原理生成的随机数都是伪随机数。
注:这里生成的随机数所处的分布为0-1区间上的均匀分布。我们需要的随机数序列应具有非退化性,周期长,相关系数小等优点。
2.1迭代取中法:
这里在迭代取中法中介绍平方取中法,其迭代式如下:
Xn+1=(Xn^2/10^s)(mod 10^2s)
Rn+1=Xn+1/10^2s
其中,Xn+1是迭代算子,而Rn+1则是每次需要产生的随机数 。
第一个式子表示的是将Xn平方后右移s位,并截右端的2s位。
而第二个式子则是将截尾后的数字再压缩2s倍,显然:0=<Rn+1<=1.
这样的式子的构造需要深厚的数学(代数,统计学,信息学)功底,这里只是拿来用一下而已,就让我们站在大师的肩膀上前行吧。
迭代取中法有一个不良的性就是它比较容易退化成0.
平方取中法的实现:
#include <stdio.h>
#include <math.h>
#define S 2
float Xn=12345;//Seed & Iter
float Rn;//Return Val
void InitSeed(float inX0)
{
Xn=inX0;
}
/*
Xn+1=(Xn^2/10^s)(mod 10^2s)
Rn+1=Xn+1/10^2s
*/
float MyRnd()
{
Xn=(int)fmod((Xn*Xn/pow(10,S)),pow(10,2*S));//here can's use %
Rn=Xn/pow(10,2*S);
return Rn;
}
/*测试主程序,注意,这里只列举一次测试主程序,以下不再重复*/
int main()
{
int i;
FILE * debugFile;
if((debugFile=fopen("outputData.txt","w"))==NULL)
{
fprintf(stderr,"open file error!");
return -1;
}
printf("\n");
for(i=0;i<100;i++)
{
tempRnd=MyRnd();
fprintf(stdout,"%f ",tempRnd);
fprintf(debugFile,"%f ",tempRnd);
}
getchar();
return 0;
}
0.399000 0.920100 0.658400 0.349000 0.180100 0.243600 0.934000 0.235600 0.550700 0.327000 0.692900 0.011000 0.012100 0.014600 0.021300 0.045300 0.205200 0.210700 0.439400 0.307200 0.437100 0.105600 0.115100 0.324800 0.549500 0.195000 0.802500 0.400600 0.048000 0.230400 0.308400 0.511000 0.112100 0.256600 0.584300 0.140600 0.976800 0.413800 0.123000 0.512900 0.306600 0.400300 0.024000 0.057600 0.331700 0.002400 0.000500 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
容易看出其易退化成0的缺点.
2.2乘同余法:
乘同余法的迭代式如下:
Xn+1=Lamda*Xn(mod M)
Rn+1=Xn/M
各参数意义及各步的作用可参2.1
当然,这里的参数的选取是有一定的理论基础的,否则所产生的随机数的周期将较小,相关性会较大。
经过前人检验的两组性能较好的素数取模乘同余法迭代式的系数为:
1) lamda=5^5,M=2^35-31
2) lamda=7^5,M=2^31-1
相应C程序关键代码段:
double long M;//请注意,这里一定要用到double long,否则计算2^32会溢出
float MyRnd()
{
Xn=fmod(Lamda*Xn,M);//here can's use %
Rn=Xn/M;
return Rn;
}
初始化段,应有:
M=pow(2,35)-31;
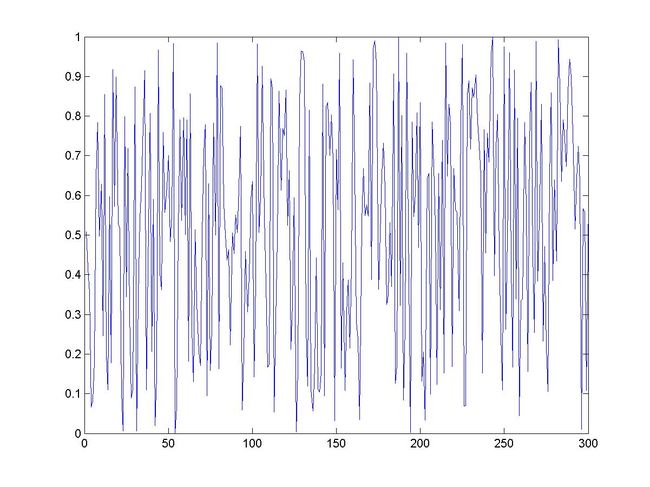
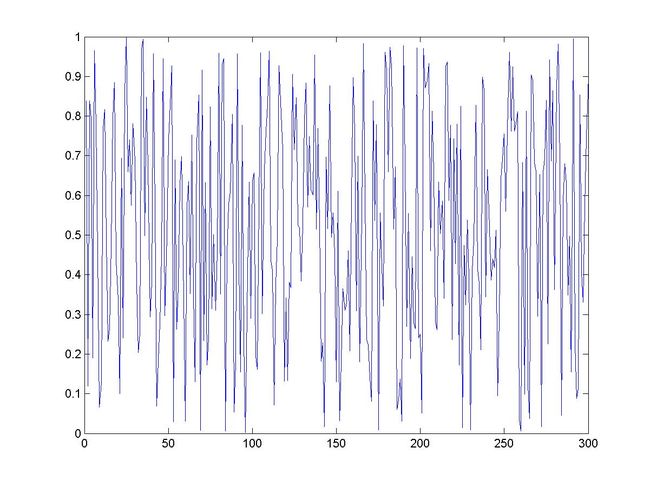
图1: 乘同余法生成的300随机数的产生序列图
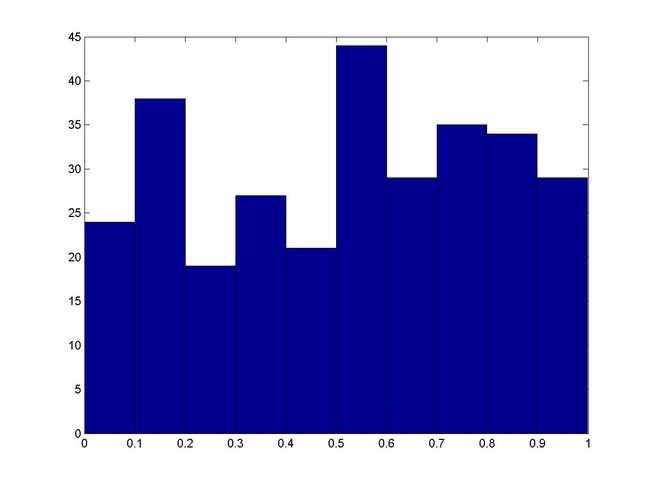
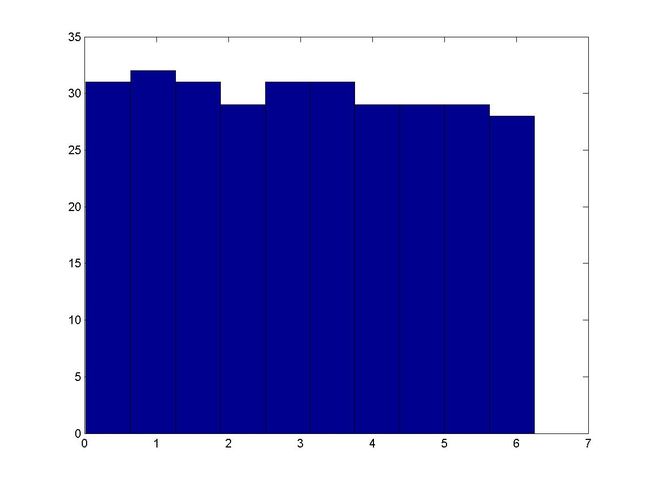
图2: 乘同余法生成的300随机数的分布情况
可以看到,该随机数生成方法所生成的随机序列比较符合0-1上的均匀分布,不过在某些数据段还有些起伏。
2.3混合同余法:
混合同余法是加同余法和乘同余法的混合形式,其迭代式如下:
Xn+1=(Lamda*Xn+Miu)%M
Rn+1=Xn/M
经前人研究表明,在M=2^q的条件下,参数lamda,miu,X0按如下选取,周期较大,概率统计特性好:
Lamda=2^c+1,c取q/2附近的数
Miu=(1/2+sqrt(3))/M
X0为任意非负整数
相应C程序关键代码段:
M=pow( 2, 32);
Lamda=pow( 2, 16)+ 1;
Miu=( 0.5+sqrt( 3)/ 6)/M;
float MyRnd()
{
Xn=fmod(Lamda*Xn+Miu,M);
Rn=Xn/M;
return Rn;
}
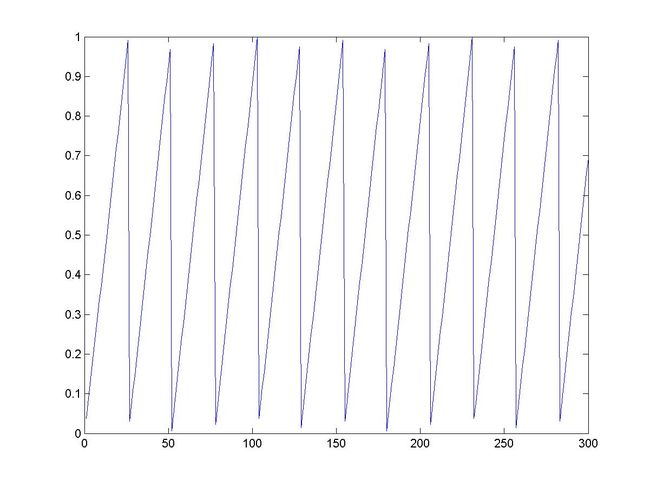
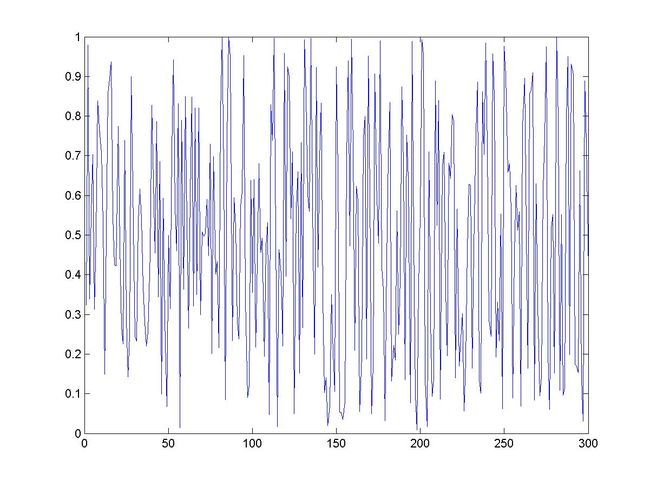
图3: 乘同余法生成的300随机数的产生序列图
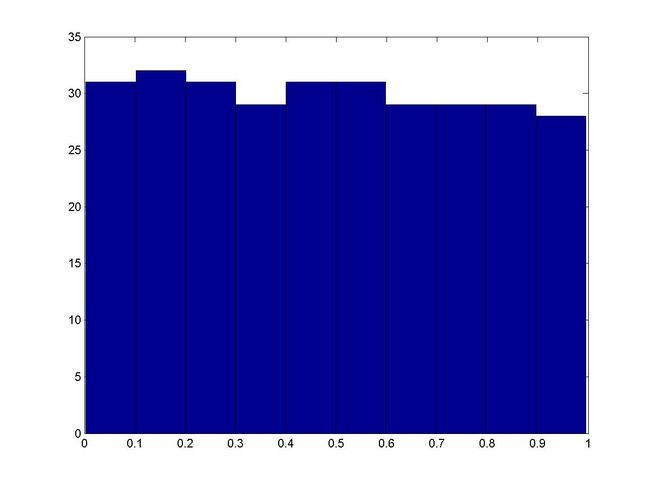
图4: 乘同余法生成的300随机数的分布情况
由图4可以看出,该种随机数生成方法已相当接近0-1上的均匀分布。但在图3中可以看出它的一个致命的弱点,那就是随机数的生成在某一周期内成线性增长的趋势,显然,在大多数场合,这种极富“规律”型的随机数是不应当使用的。
下面的概率分布型随机变量的生成,均采用乘同余法或C函数库中的随机数来生成0-1区间上的随机数。
下面将C语言中的随机数生成序列图和Matlab中的随机数生成序列图列于下面,以作对比之用:
C语言生成的300个随机数的序列图
Matlab中rand函数生成的300个随机数的序列图
可以看出:乘同余法生成的随机数序列的随机性与上述两个标准库函数相接近。
3连续型随机变量的生成:
3.1反函数法
采用概率积分变换原理,对于随机变量X的分布函数F(X)可以求其反函数,得:
Xi=G(Ri)
其中,Ri为一个0-1区间内的均匀分布的随机变量.
F(X)较简单时,求解较易,当F(X)较复杂时,需要用到较为复杂的变换技巧。
3.1.1平均分布:
例:已知炮弹对目标的方位角Fi在0-2*P内均匀分布,试用(0,1)均匀随机数变换,模拟弹着点方位角的抽样值Fi.
解: R=F(Fi)=Fi/2*PI
得Fi=G(R)=2*PI*R ,其中,R为0-1区间上的均匀分布的随机数.
程序略
试验结果:
图5:用反函数法生成的300随机数的平均分布情况
由于这里相当对0-1上的分布进行线性变换,所以变换后仍呈均匀分布是显然的。
3.1.2指数分布:
指数分布的分布函数为:
x<0时,F(x)=0 ; x>=0,F(x)=1-exp(-lamda*x)
利用反函数法,可以求得: x=-lnR/lamda
试验结果:
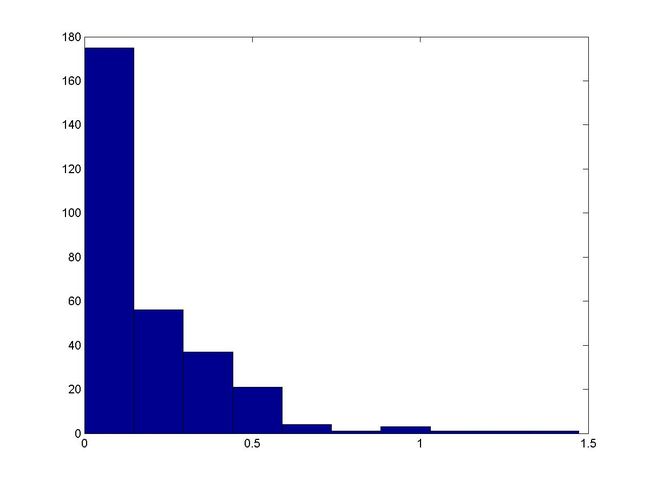
图6:用反函数法生成的300随机数的指数分布情况
可以看出,生成的随机量较好的符合了指数分布特征。
3.2正态分布随机变量的生成:
正态分布在概率统计的理论及应用中占有重要地位,因此,能产生符合正态分布的随机变量就在模拟一类的工作中占有相当重要的地位。下面介绍两种方法。
3.2.1舍选法:
这种方法便捷而有效,且具有一定的代表性,其基本思路是:
在概率密度的函数图像的外围画一个大框,然后在这个框内部产生随机点(rx,ry),根据是否落在概率密度函数的下方,来决定是否要留下这个点。
经过一定的计算变行,符合二维的正态分布的随机变量的生成可按下面的方法进行:
1)产生位于0-1区间上的两个随机数r1和r2.
2)计算u=2*r1-1,v=2*r2-1及w=u^2+v^2
3)若w>1,则返回1)
4) x=u[(-lnw)/w]^(1/2)
y=v[(-lnw)/w]^(1/2)
如果为(miu,sigma^2)正态分布,则按上述方法产生x后,x’=miu+sigma*x
由于采用基于乘同余法生成的0-1 上的随机数的正态分布随机数始终无法能过正态分布总体均值的假设检验。而采用C语言的库函数中的随机数生成函数rand()来产生0-1 上的随机数,效果较为理想。
关键程序段(funNorm返回一维的正态分布,而funNorm2则生成二维的随机分布):
float funNorm(float miu,float sigma)
{
float r1,r2;
float u,v,w;
float x,y;
do
{
r1=MyRnd();
r2=MyRnd();
u=2*r1-1;
v=2*r2-1;
w=u*u+v*v;
}while(w>1);
x=u*sqrt(((-log(w))/w));
y=v*sqrt(((-log(w))/w));
return miu+sigma*x; //also could return miu+sigma*y;
}
typedef struct
{
float x;
float y;
}sPoint;
sPoint funNorm2(float miu1,float sigma1,float miu2,float sigma2)
{
float r1,r2;
float u,v,w;
float x,y;
sPoint mPoint;
do
{
r1=rand()/(float)32767;
r2=rand()/(float)32767;
u=2*r1-1;
v=2*r2-1;
w=u*u+v*v;
}while(w>1);
x=u*sqrt(((-log(w))/w));
y=v*sqrt(((-log(w))/w));
mPoint.x=miu1+sigma1*x;
mPoint.y=miu2+sigma2*x;
return mPoint;
}
列出在Matlab下对某次试验(生成分布为N(0,1)的随机数)的检测结果:
[muhat,sigmahat,muci,sigmaci]=normfit(a)
[h,sig,ci]=ztest(a,0,1)
Output:
muhat =-0.0246 %显著性为0.95的条件下,均值的点估计。
h = 0 %接受方差为1,均值估计为0的假设检验,不能拒绝假设。
sig =0.6700 %假设的成功概率.
由此可见,在这种条件下生成的正态随机数序列基本能符合使用的要求,在精度上仍有该进的余地。
3.2.2利用中心极限定理生成符合正态分布的随机量:
根据独立同分布的中心极限定理,有:
这里,其实只要取n=12(这里,亦即生成12个0-1上的随机数序列)就会有比较好的效果。
经验证,用该种方法生成生的随机数序列同样能比较好的符合正态分布特性。
由于生成的都是标准正态分布,所以,当需要生成N(a,b)的正态分布随机量时,根据正态分布的线性变换特性,只要用x=a*x0+b即可。(其中,x0表示生成的符合N(0,1)分布的正态随机变量。方法3.1亦是如此)
4离散型随机变量的生成:
离散型随机变量的生成主要是希望得到在已知X符合某类分布的条件下,生成相应的X。
4.1符合泊松分布的随机变量的生成:
这里,采用”上限拦截”法进行测试,其本的思想是这样的:
1)在泊松分布中,求出X取何值时,p(X=k)取最大值时,设为Pxmax.
其时,这样当于求解f(x)=lamda^k/k! 在k取何值时有最大值,虽然,这道题有一定的难度,但在程序中可以能过一个循环来得到取得f(x)取最大值时的整数自变量Xmax。
2) 通过迭代,不断生成0-1区间上的随机数,当随机数<Pxmax时,则终止迭代,否则重复(2)
3) 记录迭代过程的次数,即为所需要得到的符何泊松分布的随机量。
显然,这种方法较为粗糙,在试验的过程中发现:生成的的随机量只能算是近似的服从
泊松分布,所以,更为有效的算法还有待尝试。
4.2符合二项分布的随机变量的生成:
符合二项分布的随机变量产生类似上限拦截法,不过效果要好许多,这是由二项分布的特点决定的。
具体方法如下:
设二项分布B(p,n),其中,p为每个单独事件发生的概率:
关键算法:
i=0;reTimes=0
while(i<n)
{
temp=MyRnd();//生成0-1区间上的随机变量
if(temp>1-p)
reTimes++;
i++;
}
显然,直观的看来,这种算法将每个独立的事件当作一个0-1分布来做,生成的0-1区间上的随机数,若小于1-p则不发生,否则认为发生,这样的生成方式较为合理。实验结果也验证了其合理性。
5实验结论:通过本实验,使我感受到,要生成符合要求的随机数序列,绝不是一件很轻松的事,除了要有相当的知识储备外,更应当有严谨求实的态度在其中;否则,光凭主观感觉说某些随机数的随机性好,是会在实际应用中是要栽跟头的。
有些随机数的生成仍未达到要求,有机会仍应继续被充,加深该方面理论和应用的理解。