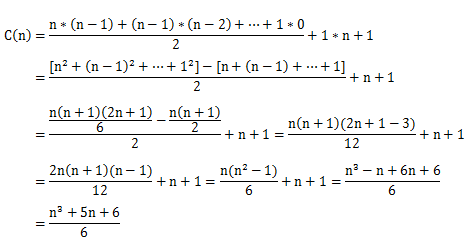HDU 1290 献给杭电五十周年校庆的礼物(空间分割)

献给杭电五十周年校庆的礼物

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Problem Description

或许你曾经牢骚满腹
或许你依然心怀忧伤
或许你近在咫尺
或许你我天各一方

对于每一个学子
母校 
永远航行在
生命的海洋

今年是我们杭电建校五十周年，这是一个值得祝福的日子。我们该送给母校一个怎样的礼物呢？对于目前的大家来说，最好的礼物当然是省赛中的好成绩，我不能参赛，就送给学校一个DOOM III球形大蛋糕吧，这可是名牌，估计要花掉我半年的银子呢。

想象着正式校庆那一天，校长亲自操刀，把这个大蛋糕分给各地赶来祝贺的校友们，大家一定很高兴，呵呵，流口水了吧...

等一等，吃蛋糕之前先考大家一个问题：如果校长大人在蛋糕上切了N刀（校长刀法极好，每一刀都是一个绝对的平面），最多可以把这个球形蛋糕切成几块呢？

做不出这个题目，没有蛋糕吃的！
为-了-母-校-，为-了-蛋-糕-（不是为了DGMM，枫之羽最会浮想联翩...），加-油-！

 

Input

输入数据包含多个测试实例，每个实例占一行，每行包含一个整数n(1<=n<=1000)，表示切的刀数。

 

Output

对于每组输入数据，请输出对应的蛋糕块数，每个测试实例输出一行。

 

Sample Input

   
   
   
   

    
    
    
    1
2
3
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    2
4
8
   
   
   
   

 

/************************************************************************/

此题是一个关于空间分割的问题，问N个平面最多可以把球体分成几个区域

若是平面分割问题，或许我们还可以通过画画图，找找规律，但空间分割，单纯靠画也是真心累，4个平面就已经让我觉得画起来够呛了

既然如此，我们何必从平面分割来推到空间分割呢，毕竟曾经一句“点构成线，线构成面，面构成体”现在可是印象深刻

好了，不闲聊，我们回到正题上，首先N条直线能把平面分成几个区域应该大家都知道吧，添加第N条直线时，最佳的画法是与之前的N-1条直线都有交点，且三条及三条以上的直线之间没有共同的交点，这样可以增加N个区域，于是就得到了这样一个式子

P(n)=P(n-1)+n    P(0)=1

那么n个式子相加便可以得到 P(n)=1+(1+2+…+n)=n(n+1)/2+1

接下来我们来考虑空间的情况，同样，为了割法最佳，我们在添加第N个平面时，需要与之前的N-1个平面都有交线，另外任意两条交线之间两两相交且无重点，这样我们新添加的这个面就已经被分割成了P(n-1)个区域，而这P(n-1)个区域可以使得整个空间增加P(n-1)块，故我们可以得到这样一个式子

C(n)=C(n-1)+P(n-1)=C(n-1)+n*(n-1)/2+1  C(0)=1

将n个式子相加便可以得到

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<stdlib.h>
#include<cmath>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 105;
const int inf = 2147483647;
const int mod = 1000000007;
int main()
{
    int n;
    while(~scanf("%d",&n))
        printf("%d\n",(n*n*n+5*n+6)/6);
    return 0;
}

菜鸟成长记