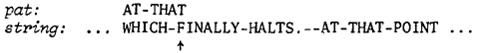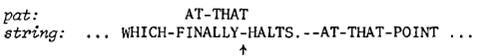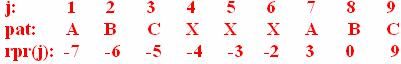Boyer-Moore 经典单模式匹配算法

O了O了！我现特想说：一个人Boyer-Moore都敢闹明白，他还有什么不敢的呢^_^

 

经典单模式匹配算法：KMP、BM；经典多模式匹配算法：AC、Wu-Manber。貌似实用中，KMP跟C库strstr()效率相当，而BM能快上3x-5x。于是小女不才花了小天的功夫来研究这个BM算法。BM如何快速匹配模式？它怎么跳跃地？我今儿一定要把大家伙儿讲明白了，讲不明白您佬跟帖，我买单，包教包会。

模式，记为pat，用j作为索引; 文本，记为string（或text），用i作为索引。

 

Input: pat, string Algorithm: BM，在string中进行pat匹配。 Output: 匹配上则返回匹配地址，否则返回-1。

 

图1

 

图1是一简单示意图。左对齐pat与string，小指针（记为p）指向对齐后的右end，开始比对。如果pat[p]= string[p]，那么小指针往左挪（挪到左end说明匹配上了），否则就要滑动pat进行重新对齐，重新对齐后，小指针当然也要跟着溜到末位进行重新比对。那么究竟怎么个滑法？分四个case：

 

1.       末位不匹配，且string[p]在pat中不存在，那么pat可以一下子右移patlen个单位。因为你一个一个右移只是徒劳，没人跟string[i]能匹配上。比如，图1中F与T不匹配，且F在pat中不存在，那么我们可以把pat右滑patlen，小指针也跟着移至末位，移动后如图2所示。

 

 

图2

 

2.       末位不匹配，但string[p]在pat中存在（如果有多个，那就找最靠右的那个），距离pat右端为delta1。那么右移pat使得它们对齐。比如，图2中减号与T不匹配，但减号存在于pat中，数数知道delta1=4，那就右移pat使得两个减号对上，移动后如图3所示。

 

 

图3

 

总结：从1、2可以得到， dealta1 = patlen,  当string[p]在patlen中不存在       = patlen – 最右边那个string[p]的位置，   当string[p]在patlen中存在   delta1()是所有字符的函数，例如pat和string对应26个字母，那么dealta1(‘a’)…dealta1(‘z’)。只需扫描一下pat，就能记录下值了。别地儿管这个叫“坏字符规则”。

 

3.       末m位都匹配上了(m<patlen)，但未匹配完，如图4中的三个示例，末m (m=4)位匹配上了，小指针指向的两个字符都发生了mismatch，记为mismatched char。

1)        图4中示例1，string中的c在pat中的最右出现居然还在小指针靠后的位置，总不至于为了让string中c跟pat中最右c匹配上就把pat往回倒滑一个位置吧，才不要那么瓜，遇到这种情况就让pat往右滑k=1个位置好了，此时小指针为了滑至最后需要滑k+m=5个位置。

2)        图4中示例2，string中c在pat中的最右出现在小指针前面，那好吧，就让此a跟彼a对齐吧。即让pat向右滑k=delta1(‘a’)-m=6-4=2个位置，此时小指针为了滑至最后需要滑k+m={dealta1(‘a’)-m}+m=dealta1(‘a’)=6个位置。

3)        图4中示例3，string中y在pat中未出现。那么将patlen向右移k=delta1(‘y’)-m=6-4=2个位置，此时小指针为了滑至最后需要滑dealta1(‘y’)=6个位置。

 

 

图4

 

总结：从3可以得到， pat右移位数 = 1，  当示例1             = k =delta1(‘char’)-m， 当示例2、3。. String右移位数 = k+m

 

4.         照着3那么移挺对也挺好地，但某些情况下，如图7的情况，能不能让pat右移地更快呢？图7示例1，按3的分析只能将pat右滑1位，实际上我们可以放心右滑pat成示例2的样子，然后再将小指针移至末位开始匹配。

 

 

图7

 

下面的部分会比较绕，请读者用心看。图7示例1，末m(m=3)位即abc匹配上了，记为subpat，那么pat中出现的最右abc且不由mismatched char引导的位置，记为末subpat的“重现位置”，如”gabcfabceabceabc”重现位置应该是f引导的subpat，可以理解么？因为g引导的subpat不是最右的，倒数第2个e引导的subpat是由mismatched char引导的。

于是我们引入delta2(j)函数，j是发生mismatched的位置，我们记subpat的“重现位置”为rpr(j)，那么pat应该右移k，相应地string右移k+m。如何计算k?

 

预处理pat，j=1…patlen，那么rpr(j)是指以j为mismatched的位置，以j+1…patlen为subpat的“重现位置”。 rpr(j) = max{k| k<=patlen && [pat(j+1) ... pat(patlen)]= [pat(k) ... pat(k+patlen-j-1)]           && (k<=1 || pat(k-1) != pat(j) }    rpr(patlen)=patlen。 其中对于“=”的判断，要么pat(x)=pat(j)要么pat(x)=NULL要么pat(y)=NULL。 举个例子就明白了：   下面解释rpr(j)：   上图您能接受么？呵呵，$表示空元素。例如j=1时，要跟pat[j+1]…pat[patlen]匹配，那么pat[k]…p[k+patlen-j-1]最多就是如图所示，此时k+patlen-j-1=3即k+9-1-1=3，于是k= -4，k再大您可以试试，不好使了就。其它依此类推。读者可练习求一下下面这个rpr(j)。

 

OK，如何求滑动距离k呢？现在小指针指在j的位置上，“重现位置”在rpr(j)，那么k=j+1-rpr(j)，小指针需要挪至最后所以k+m={j+1-rpr(j)}+{patlen-j}=patlen+1-rpr(j)，即有delta2(j)=patlen+1-rpr(j)。

 

总结：从3、4可以得到， 末m个元素已经匹配的情况，string需要右滑多少呢？计算delta1(string(i)),delta2(j)，谁大取谁，就说滑的越多越好，反正都有匹配不上的理由。

 

OK，现在给出算法伪码，加油，就快结束了：

 

 

实现上，可以更快一点。看到delta0()不要惊讶，它和delta1()基本相同，除了delta0(pat(patlen))被设置为>stringlen+patlen的一个数。因为1、2两种case在匹配中遇到的频率很高，我们抽出fast部分，匹配时间的70%-80%都在走fast部分。自己举个例子把伪码过一遍，不明白地方跟帖。

 

 

 

别地儿都称 “坏字符规则” “好后缀规则”，嘛回事？fatdog如是写：

 

 

 

哈哈，好不好笑？坏字符规则就是我们的delta1(char)计算，好后缀规则就是我们的delta2(j)计算，本来就一码事儿。

//预处理 计算bmGS[]和bmBC[]表；//BM的Good Suffix、Bad Character while(text<textend) {      //从当前匹配点text开始匹配关键词      for(i=m;(i>=0)&&(text[i]=pattern[i]);i--)          ;      if(i<0)      {          //匹配成功          报告一个成功的匹配;          text+=bmGS[0];//选择下一个匹配入口点      }      else  //匹配失败，此时i指示着不匹配的位置点text[i]!=pat[i]      {          //使用两种启发式方法选择下一个匹配入口点          text+=Max(bmGS[i]-m+1,bmBC[i]);      } }

BM通常是sublinear的复杂度，最好O(n/m)，最坏O(n)。一般会匹配string中的c*(i+patlen)个字符，其中c<1，并且patlen越大c越小，通常在longer pat下BM表现更出色。

 

 

学习自：1977  “A Fast String Searching Algorithm”