用MATLAB做聚类分析时非常有用的自定义距离函数和标准化函数
聚类分析中,经常遇到观测值缺失的情况.
例如统计历史降水资料时,某个月的资料缺失了,这时用MATLAB做聚类分析时,
就需要自定义距离函数,处理nan的问题.
下面是相关的MATLAB函数,里面有例子,可自行修改:
function [ nandistance ] = nandistfun( X,Y,varargin)
% A distance function for pdist,ignoring NaNs
% [ nandistance ] = nandistfun( X,Y,varargin)
% arguments :
% X: 1-by-n vector
% Y:m-by-n vector
% nandistance::m-by-1, whose kth element is the distance between X and Y(k,:).
%
% methods = {'euclidean'; 'seuclidean'; 'cityblock'; 'chebychev'; ...
% 'mahalanobis'; 'minkowski'; 'cosine'; 'correlation'; ...
% 'spearman'; 'hamming'; 'jaccard'};
%
% Example:
% >> X =[9, nan, 2, 4, 7; 8, 2, 9, nan, 5; 2, 5, 8, nan, 6];
% >> D = pdist(X,@nandistfun)
% >> D= pdist(X,@(a,b)nandistfun(a,b,'seu'))
%
% See also PDIST, SQUAREFORM, LINKAGE, SILHOUETTE, PDIST2.
%
%Author:Wu Xuping Date:2013-09-21 Version:1.0.0
[xrow,xcolumn]=size(X);
[yrow,ycolumn]=size(Y);
%可变参数的个数
nVarargs = length(varargin);
%初始化距离
nandistance=zeros(yrow,1);
if (xrow==1 && xcolumn==ycolumn)
for m=1:yrow
x1=X;%必须是行向量,不能是空向量
y1=Y(m,:);%必须是行向量,不能是空向量
b=( ~isnan(x1)) & (~isnan(y1)); %提取(x1,y1)中都不是nan的索引
A=[];
A(1,:)=x1(b);%必须是行向量,不能是空向量
A(2,:)=y1(b);%必须是行向量,不能是空向量
%计算距离
if (nVarargs>0)
nandistance(m,1) = pdist(A,varargin{:});
else
nandistance(m,1) = pdist(A); %默认'euc'
end
end
end
end
上面这个函数,包括了常用的各种距离函数.
看完了这个函数的实现方式,我想大家也可以自定义其它类型的距离函数了.
通常做聚类分析时先将数据标准化,matlab提供了zscore函数,不过不支持nans,
这时可以试试下面的函数:
function [ z ] = nanzscore( x )
%[ z ] = nanzscore( x ),ignoring NaNs
% 类似于标准化函数[ z ] = zscore( x ),忽略NaNs
% Author:wuxuping,Date:2013-09-21
nm=nanmean(x);
ns=nanstd(x);
[xrow,xcolumn]=size(x);
if ((xrow>1 )&&(xcolumn >1))
%如果是多行多列的矩阵
z=zeros(size(x));
for m=1:xrow
for n=1:xcolumn
z(m,n) = (x(m,n)- nm(n))./ns(n);
end
end
else
%如果是单行或单列的向量
if (xrow==1)
for m=1:numel(x)
z(m) = (x(m)- nm)./ns;%行向量
end
else
for m=1:numel(x)
z(m,1) = (x(m)- nm)./ns;%列向量
end
end
end
上面的标准化函数用起来和zscore是一样的,只是忽略所有的NaNs.
下面给出是一般的聚类分析过程实例:
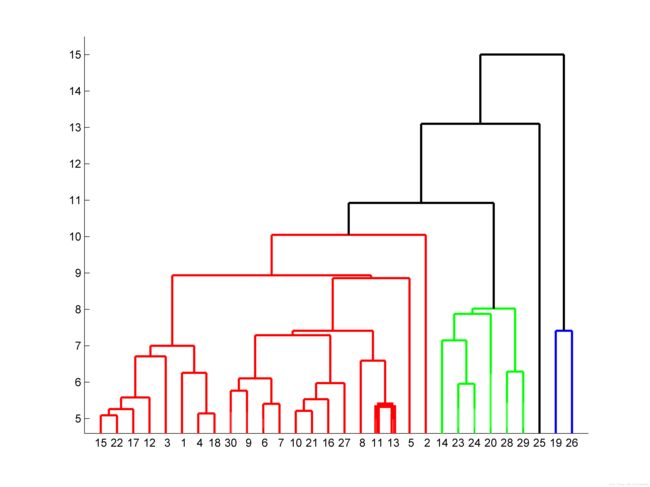
x=dlmread(filename);%80*51,八十个站点,测量了51次降水量,现在对八十个站点的降水类型进行聚类分析 %即将降水类型相同的站点聚为一类;不同类间的降水类型应该很不相同! x=nanzscore( x );%标准化 %标准化主要是测量值可能为多个项目如降水量和能见度等,而降水量和能见度的数值记录相差可能太大. %标准化其实就是把各种相差很大的量伸缩到同一个量级上来,否则计算距离时会出现大数吃小数的现象. %如果只有降水量,且采用同样的单位则无需标准化 D = pdist(x,@nandistfun);%计算距离向量,大小为:(1*3160) %Y = squareform(D,'tomatrix')%格式化距离向量为矩阵,方便查看 Z=linkage(D,'average');%采用平均距离法计算聚类,获取分层聚类树 [H,T] =dendrogram(Z,'colorthreshold','default');%绘制聚类图,返回图像对象H和聚类表T %size(T)应为80*1 numCluster=numel(H);%分类的总数,如果numCluster为29则表明将80个站点分为29个降水类型 set(H,'LineWidth',2);%将所有类的线条都加粗为2 set(H(5),'LineWidth',5);%将第五类的颜色加粗为5 find(T==5)%显示属于第五类的索引值
分层聚类树图如下:
剩下的问题是就是如何评价聚类的结果,也就是聚类的结果是否合理?对于合理的聚类,
我们知道同类的相似性一定要大,不同类之间的相似性一定要小.这个同样也可用距离来度量,当然也有用置信系数或风险系数去度量的.
第一种评价方法:对于第i类,我们计算该类中心的位置,然后该类中的所有站点到中心的距离之和的平均值记为di,
然后对所有的di求平均得dm,认为di平均值最小的聚类中同类之间的相似性是最大的,即为最合理的类.
第二种评价方法:将每一类的中心计算出来,然后将各类中心之间的距离累加,记为DM,所得的结果最大则表明该种聚类中,各类之间的差异是最大的.
第三种评价方法综合考虑同类相似性和异类的差异性,计算max(DM)/min(dm),该值取最大则表示该聚类是最合理的聚类.这在matlab中使用表象系数来求解即可.