二叉树非递归遍历
三种顺序,前、中、后序。递归版的比较好写,但当树很大时容易导致栈溢出,因此,非递归版的才更有实用价值。参考网上的一些优秀例子,自己也写了下,对后序遍历做了改进。
用栈实现,模拟递归过程,前,中序不需要加标志位,而后序则麻烦一些,需要加标志位,标记节点是否二次入栈。
代码注释懒的写,直接把函数流程图画上来:
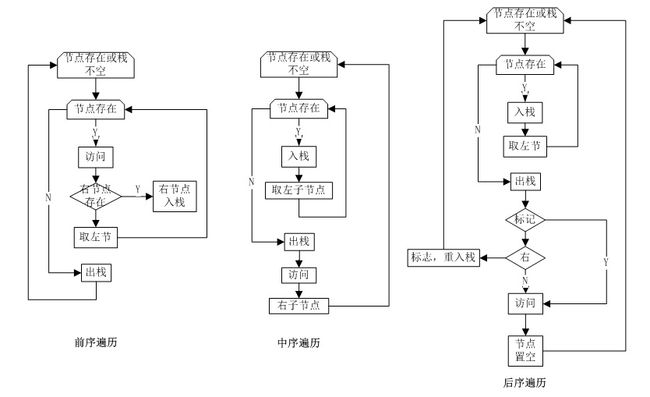
//代码
#include "
// HelloWorld.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <time.h>
#include <math.h>
#include <iomanip>
void Print(int* R,int N) //打印二叉树数组
{
for (int i=0;i<N;++i)
{
std::cout<<R[i]<<", ";
}
}
typedef struct tagTREE
{
int val;
tagTREE* left;
tagTREE* right;
tagTREE* parent; //一下次定义多个指针变量不行?
bool isVisited;
}TREE;
template<class T>
class Stack
{
private:
typedef struct tagLINK
{
T val;
tagLINK* pNext;
}LINK;
LINK* head;
public:
Stack():head(0){}
void push( T t )
{
LINK* pLINK = new LINK();
pLINK->val = t;
pLINK->pNext = head;
head = pLINK;
}
T pop()
{
if (head != NULL)
{
T val = head->val;
LINK* temp = head->pNext;
delete head;
head = temp;
return val;
}
return NULL;
}
bool empty()
{
return head ? false : true;
}
};
//按数组里指定的数值生成任意二叉树结构,数组里缺失的数值表示该索引的节点没有
void CreateTree(TREE** node, int a[], int N )
{
//预处理,记录节点在全部节点中的索引,而不是其真正位置号
cout<<endl;
int* arr = new int[a[N-1]];
for (int i=0;i<a[N-1];++i)
{
arr[ i ] = 0;
}
int k=0;
for (int i=0;i<N;++i)
{
arr[ a[i]-1 ] = i;
}
TREE* arrTree = new TREE[N];
//root
arrTree[0].parent = NULL;
for (int i=1;i<=N;++i)
{
arrTree[i-1].val = a[i-1];
arrTree[i-1].isVisited = false;
int parentIdx = int(a[i-1] / 2);
if( parentIdx == 0 )
arrTree[i-1].parent = NULL;
else
arrTree[i-1].parent = &arrTree[ arr[ parentIdx-1 ] ];
int leftIdx = int(a[i-1] * 2 );
int rightIdx = leftIdx + 1;
if ( leftIdx > a[N-1] || arr[leftIdx-1] == 0 )
{
arrTree[i-1].left = NULL;
}
else
{
arrTree[i-1].left = &arrTree[ arr[ leftIdx-1 ] ];
}
if ( rightIdx > a[N-1] || arr[rightIdx-1] == 0 )
{
arrTree[i-1].right = NULL;
}
else
{
arrTree[i-1].right = &arrTree[ arr[ rightIdx-1 ] ];
}
}
*node = arrTree;
//test
for (int i=1;i<=N;++i)
{
cout<<"val="<<arrTree[i-1].val;
cout<<" left=";
if (arrTree[i-1].left)
{
cout<<arrTree[i-1].left->val;
}
cout<<" right=";
if (arrTree[i-1].right)
{
cout<<arrTree[i-1].right->val;
}
cout<<" parent=";
if (arrTree[i-1].parent)
{
cout<<arrTree[i-1].parent->val;
}
cout<<endl;
}
}
void NonRecursePreorder(TREE* node)
{
Stack<TREE*> stk;
while( node || !stk.empty() )
{
while(node)
{
cout<<node->val<<",";
if( node->right )
stk.push(node->right);
node = node->left;
}
node = stk.pop();
}
}
void NonRecurseInorder(TREE* node)
{
Stack<TREE*> stk;
while( node || !stk.empty())
{
while(node) //当节点存在时,先将它入栈,然后不停的索引左子节点
{
stk.push(node);
node = node->left;
} //当无左子节点时,最后一个入栈的节点正是要访问的
node = stk.pop();
cout<<node->val<<",";
node = node->right; //取出右节点,返回循环,如果右节点为空,则需要继续出栈
}
}
void NonRecursePostorder(TREE* node)
{
Stack<TREE*> stk;
while (node || !stk.empty())
{
while(node)
{
stk.push(node);
node = node->left;
}
node = stk.pop();
if (!node->isVisited)
{
if (node->right)
{
node->isVisited = true;
stk.push(node);
node = node->right;
continue;
}
}
cout<<node->val<<",";
node = NULL;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
const int M = 16;
int arr[M] = { 1,2,3,4,5,7,8,9,11,14,15,17,18,23,28,29 };
TREE* node;
CreateTree(&node,arr,M);
cout<<"Mid:"<<endl;
NonRecurseInorder(node);
cout<<"Front:"<<endl;
NonRecursePreorder(node);
cout<<"Back:"<<endl;
NonRecursePostorder(node);
return 0;
}
输出结果:
val=1 left=2 right=3 parent=
val=2 left=4 right=5 parent=1
val=3 left= right=7 parent=1
val=4 left=8 right=9 parent=2
val=5 left= right=11 parent=2
val=7 left=14 right=15 parent=3
val=8 left= right=17 parent=4
val=9 left=18 right= parent=4
val=11 left= right=23 parent=5
val=14 left=28 right=29 parent=7
val=15 left= right= parent=7
val=17 left= right= parent=8
val=18 left= right= parent=9
val=23 left= right= parent=11
val=28 left= right= parent=14
val=29 left= right= parent=14
Mid:
8,17,4,18,9,2,5,11,23,1,3,28,14,29,7,15,Front:
1,2,4,8,17,9,18,5,11,23,3,7,14,28,29,15,Back:
17,8,18,9,4,23,11,5,2,28,29,14,15,7,3,1,请按任意键继续. . .
参考文献:
http://blog.csdn.net/kofsky/article/details/2886453