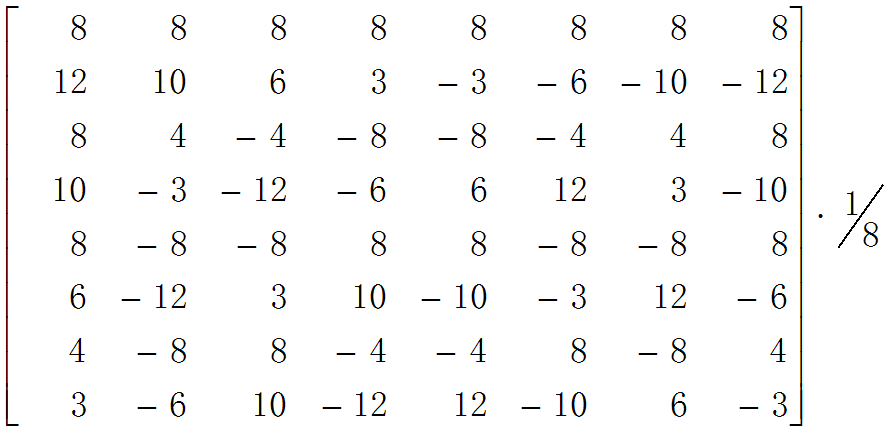H.264 Transform

      变换是视频、图像编码的核心部分。目前所采用的变换算法都是从傅里叶变换演变而来。单纯的变换并不会导致视频（图像）的码率变小，反而会增大。但是非常巧妙的一点是：变换把图像从空域转换成的时域，把由色块组成的图像变为由基准色调与图像细节组成；低频代表图片的基准色调，高频代表图像细节，类比电路中的基频与谐波。变换会使得图像的低频系数集中于某一点（左上角），频率向右下角递增。一般来说，4x4大小的图像大多只是颜色平缓的色块，不会有太多的细节，因此低频系数会较大，而高频系数较小。另外，人的眼睛对于高频系数，即图像细节，并不会特别敏感。因此，通过量化可以去掉很大一部分小的高频系数。

 

Dispersed Consine Transform

      目前视频编码中采用的变换算法是离散余项变换。根据DCT变换的定义，其变换公式可以写成：

$Y=AXA^T$

A是正交矩阵，满足$A^TA=I$.

在4x4的DCT变换中：

$ A=\begin{bmatrix}
\frac{1}{2}cos(0) & \frac{1}{2}cos(0) & \frac{1}{2}cos(0) & \frac{1}{2}cos(0)\\
\sqrt{\frac{1}{2}}cos(\frac{\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{3\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{5\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{7\pi}{8})\\
\sqrt{\frac{1}{2}}cos(\frac{2\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{6\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{10\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{14\pi}{8})\\
\sqrt{\frac{1}{2}}cos(\frac{3\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{9\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{15\pi}{8}) & \sqrt{\frac{1}{2}}cos(\frac{21\pi}{8})
\end{bmatrix}$

 

设$a = \frac{1}{2}$，$b = \sqrt{\frac{1}{2}}cos(\frac{\pi}{8})$，$c = \sqrt{\frac{1}{2}}cos(\frac{3\pi}{8})$，并由余弦函数的周期性和对称性可得：

$Y=AXA^T=\begin{bmatrix}
a & a & a & a\\
b & c & -c & b\\
a & -a & -a & a\\
c & -b & b & -c
\end{bmatrix}\begin{bmatrix}
x_{00} & x_{01} & x_{02} & x_{03}\\
x_{10} & x_{11} & x_{12} & x_{13}\\
x_{20} & x_{21} & x_{22} & x_{23}\\
x_{30} & x_{31} & x_{32} & x_33
\end{bmatrix}\begin{bmatrix}
a & b & a & c\\
a & c & -a & -b\\
a & -c & -a & b\\
a & -b & a & -c
\end{bmatrix}$

 

其逆变换（IDCT）的公式为：

$X=A^TYA$

容易验证，A可以分解成：

$A=BC=\begin{bmatrix}
a & 0 & 0 & 0\\
0 & b & 0 & 0\\
0 & 0 & a & 0\\
0 & 0 & 0 & b
\end{bmatrix}\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & d & -d & -1\\
1 & -1 & -1 & 1\\
d & -1 & 1 & -d
\end{bmatrix}$

 

 

其中$d = c/b$，B为对角矩阵。将上式带入变换表达式，可得：

$Y=BCXC^TB=
\begin{bmatrix}
a & 0 & 0 & 0\\
0 & b & 0 & 0\\
0 & 0 & a & 0\\
0 & 0 & 0 & b
\end{bmatrix}
\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & d & -d & -1\\
1 & -1 & -1 & 1\\
d & -1 & 1 & -d
\end{bmatrix}
\begin{bmatrix}
x_{00} & x_{01} & x_{02} & x_{03}\\
x_{10} & x_{11} & x_{12} & x_{13}\\
x_{20} & x_{21} & x_{22} & x_{23}\\
x_{30} & x_{31} & x_{32} & x_33
\end{bmatrix}
\begin{bmatrix}
1 & 1 & 1 & d\\
1 & d & -1 & -1\\
1 & -d & -1 & 1\\
1 & -1 & 1 & -d
\end{bmatrix}
\begin{bmatrix}
a & 0 & 0 & 0\\
0 & b & 0 & 0\\
0 & 0 & a & 0\\
0 & 0 & 0 & b
\end{bmatrix}$

 

 

因为B为对角矩阵，容易证明上式可写成：

$Y=BCXC^TB=
\begin{Bmatrix}
\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & d & -d & -1\\
1 & -1 & -1 & 1\\
d & -1 & 1 & -d
\end{bmatrix}
\begin{bmatrix}
x_{00} & x_{01} & x_{02} & x_{03}\\
x_{10} & x_{11} & x_{12} & x_{13}\\
x_{20} & x_{21} & x_{22} & x_{23}\\
x_{30} & x_{31} & x_{32} & x_33
\end{bmatrix}
\begin{bmatrix}
1 & 1 & 1 & d\\
1 & d & -1 & -1\\
1 & -d & -1 & 1\\
1 & -1 & 1 & -d
\end{bmatrix}
\end{Bmatrix}
\bigotimes
\begin{bmatrix}
a^2 & ab & a^2 & ab\\
ab & b^2 & ab & b^2\\
a^2 & ab & a^2 & ab\\
ab & b^2 & ab & b^2
\end{bmatrix}$

 

      其中运算符$\bigotimes$代表点乘，即$CXC^T$结果中的每个元素乘以矩阵$E$中对应位置上的对应元素。这里A中的a,b和c都是实数，变换的运算都在实数域中进行。其中$d=0.414213…$。考虑到计算机中，实数计算的复杂度，精确度的问题，同时因为在计算机中图像的像素值都是用整数表示，可对DCT进行改造，在牺牲一小部分压缩率的情况下，将变换改造成整数域中的运算。

      1.把$\bigotimes$后的部分合并到量化步骤中去，这里就只剩下d会对变换造成影响。

      2.选择一个接近0.414213的分数，可能的选择有7/16,3/8,1/2。标准选择d=1/2。这样可以避免在用像素值进行转换计算时出现截断误差（矩阵中出现非整数运算）。

      3.为了保证选择$d=1/2$后变换可逆，需要保持$A$的正交性，$A^TA=I$成立。我们保持$a=1/2$，可以解得

$b=\sqrt{\frac{1}{2(1+d^2)}}=\sqrt{2/5}$

      这样，得到修改后的变换公式：

$Y=
\begin{Bmatrix}
\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & \frac{1}{2} & -\frac{1}{2} & -1\\
1 & -1 & -1 & 1\\
\frac{1}{2} & -1 & 1 & -\frac{1}{2}
\end{bmatrix}
X
\begin{bmatrix}
1 & 1 & 1 & \frac{1}{2}\\
1 & \frac{1}{2} & -1 & -1\\
1 & -\frac{1}{2} & -1 & 1\\
1 & -1 & 1 & -\frac{1}{2}
\end{bmatrix}
\end{Bmatrix}
\bigotimes
\begin{bmatrix}
a^2 & ab & a^2 & ab\\
ab & b^2 & ab & b^2\\
a^2 & ab & a^2 & ab\\
ab & b^2 & ab & b^2
\end{bmatrix}$

      上式中还有个问题，就是乘以1/2的运算还不是在整数域中，这样会产生截断误差。因此，将1/2提到矩阵外面，并与右边的点乘合并。

$Y=
\begin{Bmatrix}
\begin{bmatrix}
1 & 1 & 1 & 1\\
2 & 1 & -1 & -2\\
1 & -1 & -1 & 1\\
1 & -2 & 2 & -1
\end{bmatrix}
X
\begin{bmatrix}
1 & 2 & 1 & 1\\
1 & 1 & -1 & -2\\
1 & -1 & -1 & 2\\
1 & -2 & 1 & -1
\end{bmatrix}
\end{Bmatrix}
\bigotimes
\begin{bmatrix}
a^2 & \frac{ab}{2} & a^2 & \frac{ab}{2}\\
\frac{ab}{2} & \frac{b^2}{4} & \frac{ab}{2} & \frac{b^2}{4}\\
a^2 & \frac{ab}{2} & a^2 & ab\\
\frac{ab}{2} & \frac{b^2}{4} & \frac{ab}{2} & \frac{b^2}{4}
\end{bmatrix}$

       这样就得到了H.264中所用到的整数变换公式，注意到所有的运算都在整数域中进行。其变换核$C_fXC_f^T$仅用加减法和左移即可实现，无需任何乘法（在硬件处理时，无需乘法器）。后面的$\bigotimes$运算也可以方便地合并到后面的量化过程中去。

 

整数DCT蝶形算法

       以上的整数DCT运算中三个矩阵$C,X,C^T$都是4x4的二维矩阵，可以按照以下方法分解成一维计算：

$CXC^T=(CX)C^T \qquad \qquad= 
\begin{pmatrix}C\begin{bmatrix}
x_{00} & x_{01} & x_{02} & x_{03}\\
x_{10} & x_{11} & x_{12} & x_{13}\\
x_{20} & x_{21} & x_{22} & x_{23}\\
x_{30} & x_{31} & x_{32} & x_{33}
\end{bmatrix}
\end{pmatrix}
C^T$
$ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad=\begin{bmatrix}
C\begin{bmatrix}
x_{00} \\
x_{10} \\
x_{20} \\
x_{30}
\end{bmatrix}
,C\begin{bmatrix}
x_{01} \\
x_{11} \\
x_{21} \\
x_{31}
\end{bmatrix}
,C\begin{bmatrix}
x_{02} \\
x_{12} \\
x_{22} \\
x_{32}
\end{bmatrix}
,C\begin{bmatrix}
x_{03} \\
x_{13} \\
x_{23} \\
x_{33}
\end{bmatrix}
\end{bmatrix}
C^T$
$ \qquad \qquad \qquad \qquad \quad=\begin{bmatrix}
y_{00} & y_{01} & y_{02} & y_{03}\\
y_{10} & y_{11} & y_{12} & y_{13}\\
y_{20} & y_{21} & y_{22} & y_{23}\\
y_{30} & y_{31} & y_{32} & y_{33}
\end{bmatrix}C^T$
$ =MC^T$
$ \qquad \qquad \qquad \qquad \qquad \quad=\begin{bmatrix}
\begin{bmatrix} y_{00} & y_{01} & y_{02} & y_{03} \end{bmatrix} &C^T \\
\begin{bmatrix} y_{10} & y_{11} & y_{12} & y_{13} \end{bmatrix} &C^T \\
\begin{bmatrix} y_{20} & y_{21} & y_{22} & y_{23} \end{bmatrix} &C^T \\
\begin{bmatrix} y_{30} & y_{31} & y_{32} & y_{33} \end{bmatrix} &C^T
\end{bmatrix}$

 

 

为了减少运算，其每一步一维运算都可以采用蝶形算法，减少重复计算量。以4x4DCT的第一步对X的第一列进行一维变换为例，其运算过程可用下式表示：

\begin{align*}
&y_{10} = x_{00} + x_{10} + x_{20} + x_{30} \\
&y_{20} = 2x_{00} + x_{10} - x_{20} - 2x_{30} \\
&y_{30} = x_{00} - x_{10} - x_{20} + x_{30} \\
&y_{40} = x_{00} - 2x_{10} + 2x_{20} - x_{30}
\end{align*}

其中有12次加法，4次左移。其蝶形算法如下所示：

\begin{align*}
&m_0 = x_{00} + x_{30} \\
&m_3 = x_{00} – x_{30} \\
&m_1 = x_{10} + x_{20} \\
&m_2 = x_{10} – x_{20} \\
&y_{00} = m_0 + m_1 \\
&y_{20} = m_0 – m_1 \\
&y_{10} = m_2 + (m_3<<1) \\
&y_{30} = m_3 – (m_2<<1)
\end{align*}

其中有8次加法，2次左移。

 

 

 

 

IDCT蝶形算法如下所示（对矩阵第一列进行一维变换）：

\begin{align*}
&m_0 = y_0 + y_2 \\
&m_1 = y_0 – y_2 \\
&m_2 = (y_1>>1) – y_3 \\
&m_3 = y_1 + (y_3 >> 1) \\
&x_0 = m_0 + m_3 \\
&x_3 = m_0 – m_3 \\
&x_1 = m_1 + m_2 \\
&x_2 = m_1 – m_2
\end{align*}

 

Hadamard Transform

      哈达玛变换在h.264中是专门用于转换直流系数的，这是一个可选的变换。变化平缓的画面采用这种变换方式相对于DCT来说可以减少计算步骤。

4x4哈达玛变换如下所示（主要用于亮度直流系数）：

$Y^{D4} = \begin{Bmatrix}
\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & 1 & -1 & -1\\
1 & -1 & -1 & 1\\
1 & -1 & 1 & -1
\end{bmatrix} & X^{D4} & \begin{bmatrix}
1 & 1 & 1 & 1\\
1 & 1 & -1 & -1\\
1 & -1 & -1 & 1\\
1 & -1 & 1 & -1
\end{bmatrix}
\end{Bmatrix}\frac{1}{2}$

4x4哈达玛逆变换如下所示:

$X^{D4} = \begin{Bmatrix}
\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & 1 & -1 & -1\\
1 & -1 & -1 & 1\\
1 & -1 & 1 & -1
\end{bmatrix} & Y^{D4} & \begin{bmatrix}
1 & 1 & 1 & 1\\
1 & 1 & -1 & -1\\
1 & -1 & -1 & 1\\
1 & -1 & 1 & -1
\end{bmatrix}
\end{Bmatrix}\frac{1}{2}$

2x2哈达玛变换如下所示（主要用于色度直流系数）:

$Y^{D2} = \begin{bmatrix}
1 & 1\\
1 & -1
\end{bmatrix}X^{D2}\begin{bmatrix}
1 & 1\\
1 & -1
\end{bmatrix}$

2x2哈达玛逆变换如下所示：

$X^{D2} = \begin{bmatrix}
1 & 1\\
1 & -1
\end{bmatrix}Y^{D2}\begin{bmatrix}
1 & 1\\
1 & -1
\end{bmatrix}$

 

可见哈达玛变换的正逆变换是完全一致的，用的是同一矩阵

4x4哈达吗变换蝶形算法如下所示（对矩阵第一列进行一维变换）：

\begin{align*}
&m_0 = x_0 + x_3 \\
&m_1 = x_1 + x_2 \\
&m_2 = x_1 – x_2 \\
&m_3 = x_0 – x_3 \\
&y_0 = m_0 + m_1 \\
&y_2 = m_0 – m_1 \\
&y_1 = m_2 + m_3 \\
&y_3 = m_3 – m_2
\end{align*}

 

8x8 DCT Transform

       矩阵如下：

 

蝶形算法（以下为仅对第一列进行矩阵运算）：

 

\begin{align*}
&a[0] = in[0] + in[7]; \\
&a[1] = in[1] + in[6]; \\
&a[2] = in[2] + in[5]; \\
&a[3] = in[3] + in[4];
\end{align*}

 

\begin{align*}
&b[0] = a[0] + a[3]; \\
&b[1] = a[1] + a[2]; \\
&b[2] = a[0] - a[3]; \\
&b[3] = a[1] - a[2];
\end{align*}

  

\begin{align*}
&a[4] = in[0] - in[7]; \\
&a[5] = in[1] - in[6]; \\
&a[6] = in[2] - in[5]; \\
&a[7] = in[3] - in[4];
\end{align*}

 

\begin{align*}
&b[4]= a[5] + a[6] + ((a[4]>>1) + a[4]); \\
&b[5]= a[4] - a[7] - ((a[6]>>1) + a[6]); \\
&b[6]= a[4] + a[7] - ((a[5]>>1) + a[5]); \\
&b[7]= a[5] - a[6] + ((a[7]>>1) + a[7]);
\end{align*}

 

\begin{align*}
&out[0] = b[0] + b[1]; \\
&out[2] = b[2] + (b[3]>>1); \\
&out[4] = b[0] - b[1]; \\
&out[6] = (b[2]>>1) - b[3]; \\
&out[1] = b[4] + (b[7]>>2); \\
&out[3] = b[5] + (b[6]>>2); \\
&out[5] = b[6] - (b[5]>>2); \\
&out[7] = - b[7] + (b[4]>>2);
\end{align*}

 

      8x8逆运算蝶形算法：

\begin{align*}
&a[0] = in[0] + in[4]; \\
&a[4] = in[0] - in[4]; \\
&a[2] = (in[2]>>1) - in[6]; \\
&a[6] = in[2] + (in[6]>>1);
\end{align*}

 

\begin{align*}
&b[0] = a[0] + a[6]; \\
&b[2] = a[4] + a[2]; \\
&b[4] = a[4] - a[2]; \\
&b[6] = a[0] - a[6];
\end{align*}

 

\begin{align*}
&a[1] = -in[3] + in[5] - in[7] - (in[7]>>1); \\
&a[3] = in[1] + in[7] - in[3] - (in[3]>>1); \\
&a[5] = -in[1] + in[7] + in[5] + (in[5]>>1); \\
&a[7] = in[3] + in[5] + in[1] + (in[1]>>1);
\end{align*}

 

\begin{align*}
&b[1] = a[1] + (a[7]>>2); \\
&b[7] = -(a[1]>>2) + a[7]; \\
&b[3] = a[3] + (a[5]>>2); \\
&b[5] = (a[3]>>2) - a[5];
\end{align*}

 

\begin{align*}
&out[0] = b[0] + b[7]; \\
&out[1] = b[2] + b[5]; \\
&out[2] = b[4] + b[3]; \\
&out[3] = b[6] + b[1]; \\
&out[4] = b[6] - b[1]; \\
&out[5] = b[4] - b[3]; \\
&out[6] = b[2] - b[5]; \\
&out[7] = b[0] - b[7];
\end{align*}