基本图形生成算法
基本图形生成算法
一.目的:
1.学习使用MFC的图形编程。
2.了解光栅显示的原理及基本图元线段和圆弧的生成算法。
二.内容:
1.实现DDA直线段生成算法。
2.实现Bresenham直线段生成算法。
3.实现Bresenham圆弧生成算法。
三.要求:
1.构建MFC工程:
工程名:CgLineDraw和CgCircleDraw。
选择单文档MFC框架结构:
.app为应用程序;.doc为文档,用来存放数据;.view用来绘制文档数据图形;
.MainFrame为主窗体。
2.添加图形实验程序,修改View类,显示绘制OnDraw()。
3.建立坐标系:
(1)以屏幕中心为原点(0,0),X轴为横轴,Y轴为竖轴;
(2)生成实例占据八个8分圆;
(3)分别用DDA算法和Bresenham算法绘制直线段,重复绘制100次,比较两种算法绘制直线段的效率和光滑程度,并在屏幕上显示出来。
(4)用Bresenham算法绘制完整的圆和任意角度的圆弧。
四.步骤:
(1)算法介绍:
i.数值微分法(DDA算法):直线扫描转换的最简单方法是先算出直线的斜率k=Δy/Δx,其中,Δx=x1-x0, Δy=y1-y0,(x0,y0)和(x1,y1)分别是直线的端点坐标。然后,从直线的起点开始,确定最佳逼近于直线的y坐标。假定端点坐标均为整数,让x从起点到终点变化,每步递增1,计算对应的y坐标,y=kx+B,并取象素(x,round(y))。
DDAline(int x1,int y1, int x2, int y2, CDC *pDC)
{
int i,step;
float x,y,dx,dy;
step = abs(x2-x1) > abs(y2-y1) ?
abs(x2-x1) :abs(y2-y1);
dx = (float) (x2-x1) / step;
dy = (float) (y2-y1) / step;
x = x1 + 0.5;
y = y1 + 0.5;
for (i = 0; i <= step; i++) {
pDC->SetPixel(m_wndWidth/2+(int)x,
m_wndHeight/2-(int)y,RGB(255,0,0));
x += dx;
y += dy;
}
}
ii.Bresenham画线算法:通过在每列象素中确定与理想直线最近的象素来进行直线的扫描转换的。原理是过各行,各列象素中心构造一组虚拟网格线,按直线起点到终点的顺序计算直线与各垂直网格线的交点,然后确定该列象素中与此交点最近的象素。
Bline(int x1, int y1, int x2, int y2, CDC *pDC)
{
int i,x,y,e,dx,dy,xSign,ySign,interChange = 0;
dx=abs(x2-x1);
dy=abs(y2-y1);
if(dy>dx){
interChange=1;
e=dx;dx=dy;dy=e;
}
xSign=(x2-x1) ? 1 : -1;
ySign=(y2-y1) ? 1 : -1;
x=x1;
y=y1;
e=2*dy-dx;
for(i=0;i<=dx;i++)
{
pDC->SetPixel(m_wndWidth/2+x,m_wndHeight/2+y,RGB(0,0,255));
pDC->SetPixel(m_wndWidth/2+x,m_wndHeight/2-y,RGB(0,0,255));
pDC->SetPixel(m_wndWidth/2-x,m_wndHeight/2+y,RGB(0,0,255));
pDC->SetPixel(m_wndWidth/2-x,m_wndHeight/2-y,RGB(0,0,255));
if(e>=0)
{
e=e-2*dx;
if(interChange)
x=x+xSign;
else
y=y+ySign;
}
if(!interChange)
x=x+xSign;
else
{
y=y+ySign;
}
e=e+2*dy;
}
}
iii.Bresenham画圆算法:圆心在原点,半径为R的第一个四分圆。取(0,R)为起点,按顺时针方向生成圆。从这段圆弧的任意一点出发,按顺时针方向生成圆时,为了最佳逼近该圆,下一象素的取法只有三种可能的选择:正右方象素,右下方象素和正下方象素。分别记为H,D和V。这三个象素中,与理想圆弧最近者为所求象素。理想圆弧与这三个候选点之间的关系只有下列五种情况:
1. H,D,V全在圆内;
2. H在圆外,D,V在圆内;
3. D在圆上,H在圆外,V在圆内;
4. H,D在圆外,V在圆内;
5. H,D,V全在圆外。
上述三点到圆心的距离平方与圆弧上一点到圆心的距离平方之差分别为:
ΔH=(x+1)^2+(y)^2-R^2
ΔD=(x+1)^2+(y-1)^2-R^2
ΔV=(x)^2+(y-1)^2-R^2
令δHD=|ΔH|-|ΔD|,
δDV=|ΔD|-|ΔV|,计算下一象限的算法:
当ΔD>0时,若δDV<=0,则取D,否则取V;
当ΔD<0时,若δHD<=0,则取H,否则取D;
当ΔD=0时,取D。
Bcircle(int r, CDC *pDC)
{
int x,y,delta,delta1,delta2,direction;
x=0;
y=r;
delta=2*(1-r);
while(y>=0)
{
pDC->SetPixel(x+m_wndWidth/2,y+m_wndHeight/2,RGB(255,0,255));
pDC->SetPixel(-x+m_wndWidth/2,y+m_wndHeight/2,RGB(255,0,255));
pDC->SetPixel(-x+m_wndWidth/2,-y+m_wndHeight/2,RGB(255,0,255));
pDC->SetPixel(x+m_wndWidth/2,-y+m_wndHeight/2,RGB(255,0,255));
if(delta<0)
{
delta1=2*(delta+y)-1;
if(delta1<=0) direction=1;
else
direction=2;
}
else if(delta>0)
{
delta2=2*(delta-x)-1;
if(delta2<=0) direction=2;
else
direction=3;
}
else
direction=2;
switch(direction)
{
case 1:x++;
delta+=2*x+1;
break;
case 2:x++;
y--;
delta+=2*(x-y+1);
break;
case 3:y--;
delta+=(-2*y+1);
break;
}
}
}
(2)部分代码:
a.生成坐标系及两种画线算法比较:
void CCgQBlineDemoView::OnDraw(CDC* pDC)
{
CCgQBlineDemoDoc* pDoc = GetDocument();
ASSERT_VALID(pDoc);
// TODO: add draw code for native data here
pDC->MoveTo(m_wndWidth/2, 0);
pDC->LineTo(m_wndWidth/2, m_wndHeight);
pDC->MoveTo( 0, m_wndHeight/2);
pDC->LineTo(m_wndWidth, m_wndHeight/2);
clock_t start,finish;//typedef long clock_t;
double totaltime ;
char str[10];
if (pDoc->DDAlineMode)
{
start=clock();//clock():确定处理器当前时间
//for(int n=0;n<1000;n++)
//{
DDAline(0, 0, 280, 70, pDC);
DDAline(0, 0, 70, 280, pDC);
DDAline(0, 0, -280, 70, pDC);
DDAline(0, 0, -70, 280, pDC);
DDAline(0, 0, 280, -70, pDC);
DDAline(0, 0, 70, -280, pDC);
DDAline(0, 0, -280, -70, pDC);
DDAline(0, 0, -70, -280, pDC);
//}
finish=clock();
totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
}
else
{
start=clock();//clock():确定处理器当前时间
//for(int n=0;n<1000;n++)
//{
Bline(0, 0, 280,70, pDC);
Bline(0, 0, 70, 280, pDC);
Bline(0, 0, -280, 70, pDC);
Bline(0, 0, -70, 280, pDC);
Bline(0, 0, 280, -70, pDC);
Bline(0, 0, 70, -280, pDC);
Bline(0, 0, -280, -70, pDC);
Bline(0, 0, -70, -280, pDC);
//}
finish=clock();
totaltime=((double)(finish-start)/CLOCKS_PER_SEC)/1000;
}
sprintf(str,"%lf",totaltime );//转换整型a至str
pDC->TextOut(100, 100,str);
}
b.画圆算法及任意角度圆弧:
void CCgQBlineDemoView::OnDraw(CDC* pDC)
{
CCgQBlineDemoDoc* pDoc = GetDocument();
ASSERT_VALID(pDoc);
// TODO: add draw code for native data here
pDC->MoveTo(m_wndWidth/2, 0);
pDC->LineTo(m_wndWidth/2, m_wndHeight);
pDC->MoveTo( 0, m_wndHeight/2);
pDC->LineTo(m_wndWidth, m_wndHeight/2);
if (pDoc->DDAlineMode)
{
Bcircle(200, pDC);
}
else
{
Bave(250.0,-3.14/4,3.14/3,pDC);
}
}
void CCgQBlineDemoView::Bave(float r, double k1, double k2,CDC *pDC)
{
double x,y,delta,delta1,delta2,x1,x2,y1,y2,y3,y4;
int direction;
x=0;
y=r;
x1=r*cos(k1);
x2=r*cos(k2);
y1=r*sin(k1);
y2=r*sin(k2);
if(y2>=y1)
{
y3=y2;
y4=y1;
}
else
{
y3=y1;
y4=y2;
}
delta=2*(1-r);
while(y>=y3||y<=y4)
{
pDC->SetPixel(x+m_wndWidth/2,y+m_wndHeight/2,RGB(255,0,0));
pDC->SetPixel(-x+m_wndWidth/2,y+m_wndHeight/2,RGB(255,0,0));
//pDC->SetPixel(x+m_wndWidth/2,-y+m_wndHeight/2,RGB(255,0,0));
//pDC->SetPixel(-x+m_wndWidth/2,-y+m_wndHeight/2,RGB(255,0,0));
if(delta<0)
{
delta1=2*(delta+y)-1;
if(delta1<=0) direction=1;
else
direction=2;
}
else if(delta>0)
{
delta2=2*(delta-x)-1;
if(delta2<=0) direction=2;
else
direction=3;
}
else
direction=2;
switch(direction)
{
case 1:x++;
delta+=2*x+1;
break;
case 2:x++;
y--;
delta+=2*(x-y+1);
break;
case 3:y--;
delta+=(-2*y+1);
break;
}
}
五.结果及分析:
i.两种画线算法比较:
由上述结果可知,Bresenham直线段生成算法画线效率较DDA直线段生成算法要高,两者画线的平滑度基本持平。DDA直线段生成算法虽然较易理解,但效率偏低,所以两者相比Bresenham直线段生成算法相对较优。
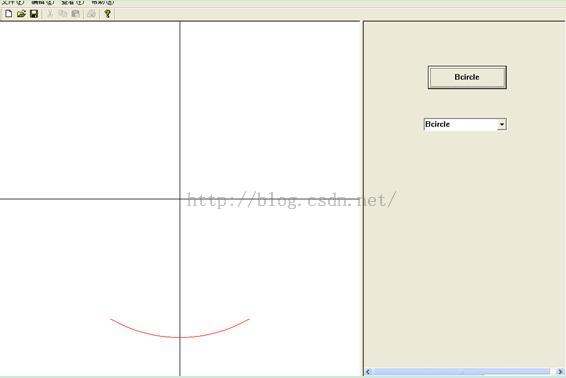
ii.B算法完整的圆和任意角度的圆: