【矩阵与行列式】矩阵和行列式学习笔记
开始从ToDoList里挑东西来杀.
感觉矩阵和行列式这两个跟很多东西都有关而且接触最少
所以先从它们开始补>w<
P.S.看了很多资料,他们对矩阵和行列式这些东西的介绍都很丧病…我会尽量用通俗的语言来写我的笔记= =如果您不喜欢这种风格QAQ那我也没办法了请隔壁看别人的吧
—————————线割分是我>w<——————————————–
什么是矩阵?
矩阵是n*m个数在n*m这个二维区域内的一个排列,是一个横纵排列的二维数字表格.
也就是说,矩阵只是一些数的一种存储形式.
通常我们使用大括号或者中括号来表示一个矩阵.
我们将矩阵中横向的元素组称为行,纵向的称为列.(P.s.Wikipedia上说这仅仅是中国大陆的叫法)
特殊的,当一个矩阵的n或者m为1时,他变成了一个向量.
通常情况下我们说的向量都是矩阵的一个列向量(即某一列上所有数的排列),那要怎么得到行向量呢?
一个矩阵转置之后的第i列的列向量就是他之前的第i行的行向量
那什么是矩阵的转置呢?
矩阵的转置和置换:
有矩阵A,将A行上元素和列上元素交换得到新的矩阵,这个新的矩阵就是矩阵A的转置,记为 AT .
例如:
它的转置是:
然而矩阵除了转置之外还有一个叫做置换的东西0-0
什么是一个矩阵的置换呢?
首先来了解一下什么叫单位矩阵.
某个n*n的矩阵的一条对角线(左上到右下的那一条,也叫主对角线)上元素全部为1,其他元素全部为0,则这个矩阵是个n阶单位矩阵.
交换一个n阶单位矩阵E的几行或几列得到的新的矩阵,称为一个n阶置换矩阵.
其实置换矩阵好像并没有什么太大的用…稍微提一下只是为了区分它和转置矩阵.
如果一个矩阵的左下角的所有元素都是0(不含主对角线),即对于任意i>j, ai,j=0 那么这个矩阵就是个 上三角矩阵.特殊的,如果主对角线上的矩阵都是1,那么这个矩阵是个 单位上三角矩阵.
跟他相反的就是下 三角矩阵和 单位下三角矩阵,我不介绍了= =
如果一个矩阵的每行每列都只有一个元素是1,其他都是0(不带对角线的n皇后那样的排列),那么称这个矩阵是个 排列矩阵.
对称矩阵: A=AT 的矩阵A是对称矩阵.
矩阵的基础运算:
矩阵的加法:
有矩阵A和矩阵B,二者都是n*m的矩阵,则他们的和矩阵C里每一个元素 Ci,j=Ai,j+Bi,j
全0矩阵是矩阵加法的单位元.
矩阵的减法:
类比加法, C=A−B , Ci,j=Ai,j−Bi,j
矩阵的倍数:
和向量的数乘运算类似,对 B=λA ,他的每一个元素 Bi,j=λ⋅Ai,j
矩阵的乘法:
矩阵乘法的要求不再是两个矩阵大小相等,他要求相乘的矩阵A和B,假设A的列数为n,则B的行数必定为n.也就是A的转置矩阵大小一定可以容纳下B矩阵或者被B矩阵容纳.官方的说法是这两个矩阵相容.
若一个矩阵A为m*n的矩阵,B为n*p的矩阵,C为他们的乘积,则
矩阵乘有一些性质:
①一个矩阵和全0矩阵的乘积是全0矩阵
②结合律:A(BC)=(AB)C
③分配律:C(A+B)=CA+CB
④单位矩阵是矩阵乘法的单位元
并没有交换律…这个你随便试试就出反例了…
好了你已经扯了千字的矩阵,可是我要看行列式.你的行列式在哪里?
QAQ不要急啊矩阵内容比较多马上就是行列式了>_<
行列式
一个矩阵A的行列式记作 det(A) ,或者 |A| .
注意:行列式只能对一个n*n的方阵而言,其他矩阵是无法构成行列式的!!!
他们的区别在哪里?
区别:行列式是一个数值,而矩阵是一个特殊的数字排列.
行列式要怎么计算呢?(偷个懒用下维基的图QAQ)

好麻烦啊…每次还得找对应位置…而且规律好复杂…
不怕不怕,看看这个↓:
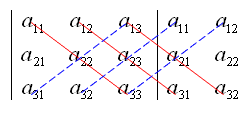
每条红线上的元素的乘积之和,减去蓝线上元素乘积之和就是行列式的值.
是不是感觉清楚多了>U<
行列式的运算也有几个性质:
① det(AT)=det(A) (毕竟是n*n方阵)
②矩阵的任意两行或两列如果交换,行列式的值要变号
③如果矩阵某两行或两列相同,行列式的值等于0
④行列式的某行或某列有一个公因子k,则 A=kA1 ,A_1为对该行或该列提出k之后剩下的那个行列式
⑤矩阵某行或某列的元素全部为0,行列式的值为0
⑥矩阵有两行或两列中每个元素对应成比例,行列式的值为0
⑦…
其实性质很多很多…在实践过程中自行脑补吧!> A <
另外对行列式有一个非常重要的公式叫Binet-Cauchy公式(比内-柯西公式)
假设矩阵A和B分别是n*m和m*n的矩阵,则
(似乎排版有点问题如果上述公式浏览不正常。。。您自己脑补一下正常的样子吧QAQ)
你问怎么来的?
这里有一个关于矩阵k阶子式的定义在前面:
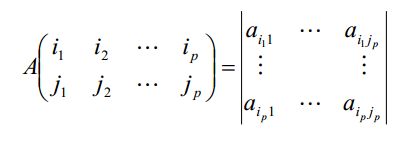
其实我并不太懂他里面蕴含的道理。。。我就当他是个普普通通的定义好了= =
扯了这么多你还是没讲怎么计算一个行列式的值啊魂淡(╯‵□′)╯︵┻━┻
不要急=- =我们马上就说
一点点来。。。
在行列式中,某一行(列)的每个元素是两个数的和,则此行列式可拆分为两个相加的行列式,如:
那么可以化成
如果对于矩阵,这个当然是错的。。。但是行列式的话就非常正确= -=
也可以用这条性质推出来:
将行列式的任意行(或一列)乘以实数k,再相应地加到另一行(或另一列)上去,则行列式的值不变。如:
有了这些可以比较直接的推出一个结论:
记作*式
(这个还是比较显然的)
于是我们可以正式开始探讨要如何求行列式的值了
已有行列式
先用高斯消元或者LU分解法把B化成一个上三角矩阵B’,同时记录一下行的交换次数S。大家应该都会吧。。到这里复杂度是 O(n3)
在接下来就有(因为我实在太懒啦不想写LaTEX了。。。所以直接从周冬论文里拷几张图下来QAQ):

(−1)s 怎么来的?见性质②
然后利用*式的结论就有

这样就得到了 O(n3) 的算法。比什么暴力代数余子式好多啦!>w<
当然还可以用分治之类的黑科技达到接近于 O(n2) 的效果。。。
————线割分是我>w<—————————————————————-
到这里矩阵和行列式的基本知识补的差不多了QUQ
虽然矩阵的秩什么的还没有好好看。。。
但是已经足够深入学一些东西了。。
不足的以后再学嘛~