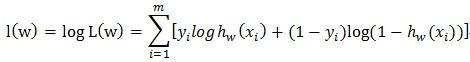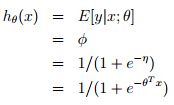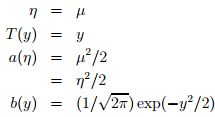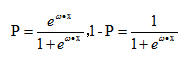广告推荐系统-逻辑回归问题导出
在广告推荐系统中，利用用户和广告之间的信息作为预测的特征
预测的过程其实就是一个二分类的问题，主要就是判定一个用户对这个广告点击或者是不点击的概率是多少
而这个过程是一个伯努利函数，整个过程是一个伯努利分布
1 广义线性模型：
指数家族分布：
是广义线性模型的基础，所以先简单了解一下指数分布族。
当固定T时，这个分布属于指数家族中的哪种分布就由a和b两个函数决定。 自然参数 η 是分布的参数。
同事广义线性模型需要满足三个条件：
如何构建GLM呢？在给定x和参数后，y的条件概率p(y|x,θ) 需要满足下面三个假设：
assum1) y | x; θ ∼ ExponentialFamily(η). 参数x,y必须是符合指数家族分布的情况
assum2) h(x) = E[y|x]. 即给定x，目标是预测T(y)的期望，通常问题中T(y)=y. 模型预测输出仍然可以认为是 E[Y] （实际上是 E[T(Y)] ，y 的分布不一定是高斯分布还有很多的别的分布， E[Y] 和 η=θTx 也不一定是简单的相等关系，它们的关系用 η=g(E[Y]) 描述，称为连接函数，其中 η 称为自然参数。
assum3) η = θTx，即η和x之间是线性的
2 逻辑回归函数：
当固定T时，这个分布属于指数家族中的哪种分布就由a和b两个函数决定。下面这种是伯努利分布，对应于逻辑回归问题，其中的
注：从上面可知
从而
，在后面用GLM导logistic regression的时候会用到这个sigmoid函数，而且从伯努利分布和逻辑回归对应的伯努利分布比较这个值就是对应的h函数。
在输出函数的时候 逻辑回归：以二分类为例，预测值y是二值的{1,0}，假设给定x和参数，y的概率分布服从伯努利分布（对应构建GLM的第一条假设，根据构建GLM的第2、3条假设可model表示成：
经典线性回归：预测值y是连续的，假设给定x和参数，y的概率分布服从高斯分布（对应构建GLM的第一条假设）。由上面高斯分布和指数家族分布的对应关系可知，η=µ，根据构建GLM的第2、3条假设可将model表示成：
4 补充说一下线性回归的计算方法（逻辑回归之后单独计算）
http://blog.csdn.net/star_liux/article/details/39646115
可以利用梯度下降最小化损失函数，也可以利用最小二乘法：
梯度下降方法：
损失函数，之后 
每次迭代，我们用当前的求出
求出等式右边的值，并覆盖得到迭代后的值。
这里
最小二乘法：
就是直接将所有样本的误差的方差相加，求其最小值，求最小值的方法也就是利用求导为0的方法：
这里需要理解一下最小二乘法和最大后验概率之间的区别：
最小二乘法主要是从训练样本中获取了n个样本，然后拟合出来一堆系数，让x和y最接近，这是距离上的接近。
而最大后验概率是获得参数让这些样本出现的概率最大。是一个概率方面的问题。
所以总结：逻辑回归和线性回归都是由广义线性模型推导出来的，之所以会有不同的形式，主要是因为数据的分布不用，在数据的分布是类似高斯分布的时候是线性回归，在伯努利分布的时候是逻辑回归，同时还会有泊松分布等等。 广义线性模型的应用最广泛的的是逻辑回归和泊松回归。逻辑回归将因变量建模为伯努利分布，输出是二值的，通常用来做二分类。泊松回归将因变量的分布建模为泊松分布，一般用来预测类似顾客数目、一个时间段内给定事件发生数目的问题。另外，对于多分类问题，将因变量建模为多项分布也是一个广义线性模型。
5 为什么会有逻辑回归
线性回归用于二分类时，首先想到下面这种形式，p是属于类别的概率：
但是这时存在的问题是：
1）等式两边的取值范围不同，右边是负无穷到正无穷，左边是[0,1]，这个分类模型的存在问题
2）实际中的很多问题，都是当x很小或很大时，对于因变量P的影响很小，当x达到中间某个阈值时，影响很大。即实际中很多问题，概率P与自变量并不是直线关系。
所以，上面这分类模型需要修整，怎么修正呢？统计学家们找到的一种方法是通过logit变换对因变量加以变换，具体如下：
从而，
这里的P完全解决了上面的两个问题。
参考：
http://www.cnblogs.com/dreamvibe/p/4259460.html
http://blog.csdn.net/lilyth_lilyth/article/details/10032993