HDU 3395 Special Fish

此题解转载自http://hi.baidu.com/aekdycoin/item/b0ae3412caf3a09b99ce33d9

很容易想到这种构图！


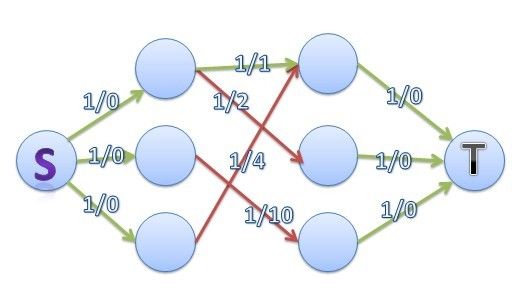
直接构造超级源S,向左边点集连边 1/0 (流量1,费用0,下同)
构造超级汇T,右边点集向T连边 1/0 (流量1,费用0)
而其他的边，都为流量1，费用为他们的原先权值

于是可以知道上图中的红色边集对应了一个最优匹配，其匹配数为3,权和为16

不过很可惜这么构图完全是错误的，只不过是YY而已


答案是2?
如果最大费用最大流，那么答案的却是2,可是答案显然是9，既取得最优权和的时候不一定匹配数最大！
(-_-我以前一直以为是最大，我蒟蒻……)
于是解决方案就不难想到(感谢SCU ISAP的大神……）

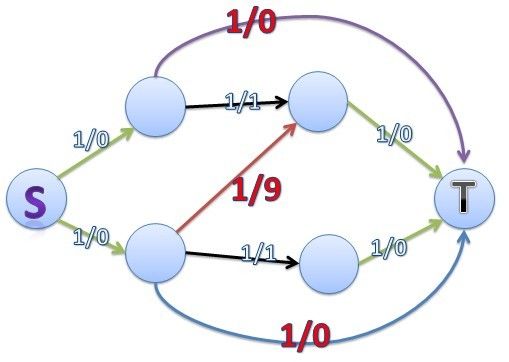
将费用变成负值，然后跑最小费用最大流就行了

学到了一点：

最大匹配不一定等于最优匹配

在cost优先的情况下，建图要满足能够让最大流相同

#include <algorithm>
#include <iostream>
#include <iomanip>
#include <cstring>
#include <climits>
#include <complex>
#include <fstream>
#include <cassert>
#include <cstdio>
#include <bitset>
#include <vector>
#include <deque>
#include <queue>
#include <stack>
#include <ctime>
#include <set>
#include <map>
#include <cmath>
#define CLR(x,y) memset(x,y,sizeof(x))
#define mp(x,y) make_pair(x,y)
#define eps 1e-9
#define INF 0x3f3f3f3f

using namespace std;

typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> pll;
typedef complex<ld> point;
typedef pair<int, int> pii;
typedef pair<pii, int> piii;

template<class T>
inline bool read(T &n)
{
    T x = 0, tmp = 1; char c = getchar();
    while((c < '0' || c > '9') && c != '-' && c != EOF) c = getchar();
    if(c == EOF) return false;
    if(c == '-') c = getchar(), tmp = -1;
    while(c >= '0' && c <= '9') x *= 10, x += (c - '0'),c = getchar();
    n = x*tmp;
    return true;
}
template <class T>
inline void write(T n)
{
    if(n < 0)
    {
        putchar('-');
        n = -n;
    }
    int len = 0,data[20];
    while(n)
    {
        data[len++] = n%10;
        n /= 10;
    }
    if(!len) data[len++] = 0;
    while(len--) putchar(data[len]+48);
}
//-----------------------------------


const int MAXN=205;

struct Node
{
    int v , w , s ;
    int next ;
} e[100005];
int val[MAXN],head[MAXN],tot;
int pre[MAXN],vis[MAXN],dis[MAXN];
int cost,flow;
char a[MAXN][MAXN];

void init()
{
	CLR(head,-1);
 	tot=0 ;
}

void addedge(int u,int v,int w,int s)
{
    e[tot].v = v ; e[tot].w = w ; e[tot].s = s ;
    e[tot].next = head[u] ; head[u] = tot++ ;
    e[tot].v = u ; e[tot].w = 0 ; e[tot].s = -s ;
    e[tot].next = head[v] ; head[v] = tot++ ;
}

int spfa(int s,int t)
{
    int u , v , i ;
    CLR(dis,INF);
    dis[s] = 0 ; vis[s] = 1 ;
    pre[s] = pre[t] = -1 ;
    queue <int> Q ;
    Q.push(s) ;
    while( !Q.empty() )
    {
        u = Q.front();
        Q.pop();
        vis[u] = 0 ;
        for(i = head[u] ; ~i  ; i = e[i].next)
        {
            v = e[i].v ;
            if( e[i].w && dis[v] > dis[u] + e[i].s )
            {
                dis[v] = dis[u] + e[i].s ;
                pre[v] = i ;
                if( !vis[v] )
                {
                    vis[v] = 1 ;
                    Q.push(v) ;
                }
            }
        }
    }
    if( pre[t] == -1 )
        return 0 ;
    return 1 ;
}

int f(int s,int t)
{
    CLR(pre,-1);
    CLR(vis,0);
    int i,mi ;
    cost=flow=0;
    while(spfa(s,t))
    {
        mi=INF ;
        for(i=pre[t]; ~i ;i=pre[e[i^1].v])
            if(e[i].w < mi)
                mi = e[i].w ;
        flow+=mi;
    	cost+=dis[t]*mi;
        for(i=pre[t]; ~i ;i=pre[e[i^1].v])
        {
            e[i].w-=mi;
            e[i^1].w+=mi;
        }
    }
    return -cost;
}

int main()
{
	int n;
	while(read(n)&&n)
	{
		init();
		int s=0,t=2*n+1;
		for(int i=1;i<=n;i++)
		{
			read(val[i]); 
			addedge(s,i,1,0);
			addedge(i+n,t,1,0);
			addedge(i,t,1,0);
		}
		for(int i=1;i<=n;i++)
			scanf("%s",a[i]+1);
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				if(a[i][j]=='1')
					addedge(i,j+n,1,-(val[i]^val[j]));		
		cout<<f(s,t)<<endl; 
	}
	return 0;
}