MATLAB信号处理仿真-基带脉冲成形的数字滤波器

http://bbs.ednchina.com/BLOG_ARTICLE_3008491.HTM

本次我们探讨另外一个在本科阶段让我们头痛的东西，通信原理之必考曲目，拼死也要背下来的内容，基带脉冲成形。然而俺对这个东西的理解和认识却是在本科以后的事情。

早年（比如[黑][社][会]大佬用摩托罗拉的手机砸人的时代）的基带成形都是用模拟电路做的，那会儿的数字电路密度极低，想想大学本科数电实验里面的各种74系列芯片，如果用这个东西拼个数字滤波器估计会疯掉。况且，就算有数字滤波器，高速高精度的ADC、DAC也是个问题。所以，早些年的数字电路课本的名字通常叫做“脉冲与数字电路”，言下之意，这东西用来处理脉冲信号的，而且，也就处理处理脉冲信号，千万别想着整太复杂的东西，那会还是一个模拟电路统治着通信系统的时代。

问题在于，除了打电话这种事情，人们还是有传送数据的需求的，比如说像寻呼机这种无线数字通信系统，更早的，比如郑君里老师在 《教与写的记忆-信号与系统评注》提到的他年轻时候的神器“1200波特数传机”这东西用现在的话讲叫做“1200波特率调制解调器”，送你一台上网用，你肯定嫌慢，但是在当时是要国家立项的重大课题。如果你愿意去一些通信原理或是信号与系统的课本里面考古，也许会看见有些习题专门探讨如何设计一个模拟的升余弦滚降滤波器。在那个时代里，数字电路的任务是把要发送的比特信息变换成脉冲信号，就是一些列各种幅度（多进制调制）的方波，我们在信号与系统的课程里知道，方波信号的带宽是无穷大的，所以后级的模拟成形滤波器负责把这些方波的频谱带宽变小，同时又要满足时域采样点无失真的准则。

我们在数字信号处理课程里面学习过IIR滤波器，而且还有“双线性变换法”，“冲击响应不变法"，以及各种让我们头晕的东西，我小时候第一次学这东西的时候在想，整这个玩意儿干嘛，后来才明白，这东西是为了用数字的方法来实现以前的模拟滤波器，模拟滤波器都是有极点的，映射到数字域中，就是IIR滤波器，那么为什么要替换掉模拟滤波器呢，有两个原因，一是为了提高通信产品的一致性，模拟元件比如电容、电阻的值是无法严格准确生产的，至于电感就是个更加不靠谱的东西，这就导致每个模拟电路元件被制造出来都不会完全一样，如果系统中大量使用模拟元件，最后误差的积累会是个大问题，所以设计者会预先在电路里面加入一些参数可调的元件，在最后的组装阶段让工人师傅看着测试仪器手动调节产品。数字电路则不同，一旦被生产出来，行为完全一致，后期的组装调试环节大为简化，所以更加有生产的效率，若你玩过红色警报、星际争霸应当知道，快速生产可是个大事情。
 

以上这个行为一致性的优点只是一方面，另一方面，更加有吸引力的是，数字电路中有一个概念叫做”等比缩小“，比如最早的计算机有房子那么大，可能连你手机里面处理器计算能力的百分之一都没有，我以前为了做某些算法，去70年代的IEEE trans 里面考古，发现某些科学家在文章的末尾贴试验数据的章节里炫富，”俺这个快速算法在拥有1M字节内存的XX型号的IBM豪华大型机上的运行时间是12秒“，俺当时感到唏嘘不已。所以，你在现在的港产警匪片里面再也看不到大佬们要专门配备一个小弟替他拿电话并且大佬还要用移动电话砸人了。

如果不是为了替换模拟时代的滤波器，或是为了适应一些特殊的自适应滤波器的需求，我是会尽量回避使用IIR滤波器的，尤其是在用FPGA作为实现手段的场合。为什么？因为这个有极点的滤波器真是对量化噪声极其敏感啊，动不动就自激振荡啊，调过一次之后被折腾的七荤八素的，后来就再也不敢用了，还是乖乖的用FIR滤波器，让领导给买个大芯片顶上先。如果是在处理器上，尤其是支持浮点的CPU，做做倒是无妨，但是也要注意滤波器如果阶数高了，IIR这东西仍然是个危险品。

所以，在数字信号处理的领域，基带成形滤波器通常的选择还是FIR，在用数字的方法进行基带成形时，需要额外注意的一个事情就是多速率，这是容易混淆的地方，这种成形滤波器有两个速率，一个是输入的符号的速率，滤波器的输入是一系列或正或负的脉冲串，这个脉冲串是由要传输的信息比特经过符号映射得到的，如果是多电平调制的方式，脉冲串会有多种幅度，最简单的映射方式是：信息比特0映射为脉冲符号-1，信息比特1映射为脉冲符号+1，这个脉冲符号是什么呢，就是“奈奎斯特准则”里面所说的“采样点无失真”的采样点，这个采样点指的就是脉冲符号。另一个速率呢，就是滤波器输出波形的采样率，根据采样定理，不能小于2倍的信号带宽，而且，有时候为了其他的原因，比如简化滤波器的设计，可能会用更高的采样率。

好了，这里我们又要展示一个跷跷板了，如同短时傅里叶变换中的时域、频域分辨率是跷跷板的两端。这个基带成形设计也有个跷跷板，让我们来看看。

所谓跷跷板，就是说，有若干个参数，而且相互之间有制约，调节了一个参数，另外的参数会随之改变，通常我们的做法是，先固定一部分，然后调节另外的，再观察调节的结果。

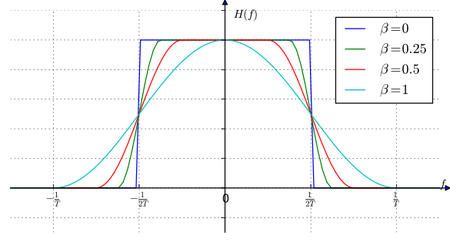
幸好，这里只有三个参数，根据通信原理的课本，当采用升余弦滚降滤波器进行成形的时候，这三个参数为：脉冲符号的速率 Rs，滚降系数beta，生成的窄带信号的带宽BW，课本上说了，BW=Rs(1+beta)/2，beta是一个介于0、1之间的小数，这个表达式很简单，它说明了这样一个事实：对于符号速率为Rs的脉冲串，如果要做到采样点无失真，用一个带限信号传输它，那么这个带限信号的带宽将会介于0.5Rs和Rs之间。这时我们跷跷板的一头是信号带宽，另一头是滤波器的频响形状，你看下面这个图，从wiki拷贝下来的，这个beta=0的时候是“砖墙”牌的理想低通啊，这可不是闹着玩的，所以说，如果要求传输固定速率的脉冲符号，要想节省带宽，就要做一个能够逼近“砖墙”的高性能滤波器，否则就得多占用带宽，这个被固定下来的符号速率呢，就是跷跷板的支点。另外，我们也可以举出另外的案例，比如说，固定下来传输带宽，这时跷跷板的两头分别是滤波器滚降系数和符号速率，这和之前的案例本质上都是一样的，不失一般性，我们下面把符号速率当做跷跷板支点来讨论。

此处，我们提供了一段代码，这段代码表达了一个1200波特/秒的脉冲串，在通过不同配置的成形滤波器后所产生信号的时频特性。
成形滤波器采用的matlab函数是rcosine，除了要配置符号率、滚降系数、输出波形的采样率之外，还需要配置一个滤波器延迟，这个参数是干啥的？通信原理的课本没说，答案在数字信号处理的课本中，因为我们知道，FIR滤波器在概念上是个多抽头的移位寄存器，问题在于一旦你通过滚降系数指定了滤波器的频响曲线形状，另外还要决定的是，你准备用多少个抽头的FIR来实现这个滤波器，抽头越多，实现的FIR的频响阻带抑制越好，但是代价是，运算量和延迟。OK，是的，你又发现有跷跷板了。注意，这个函数的延迟参数的单位是脉冲符号的个数，即相对于输入端的延迟。

下面我们开始玩弄这个代码了。

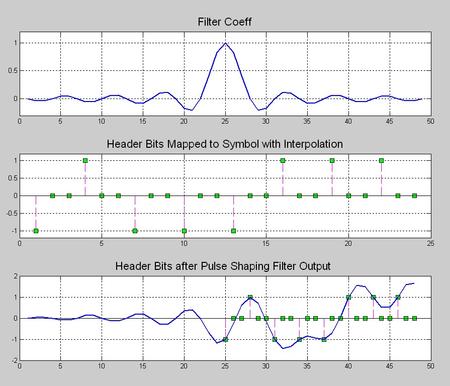
先找一个比较中庸的配置，滚降系数0.5，采样率是3倍的符号率，滤波器延迟是8（个脉冲符号），由于FIR是中心对称的，你可以看到，总共的抽头系数是3*8*2+1=49个，通过下面这张时域的图你可以看到滤波器冲击响应的时域波形，以及输入的信息比特被映射为幅度是+1、-1的脉冲串，并且，被做了补零插值当做滤波器的输入。然后，在滤波器输出信号中你看看，是否实现了采样点无失真呢（请关注那些幅度是+1，-1的样点）？这个时域的信号的原始信息比特是0x47，数字卫星标准中的著名帧头。噢，等等，你是否觉得有点眼熟，对了，其实数字化的成形滤波器就是一个多速率信号处理里面的插值滤波器，这个我们在之前的系列文章中是有讨论的。

滚降系数0.5
插图，时域波形

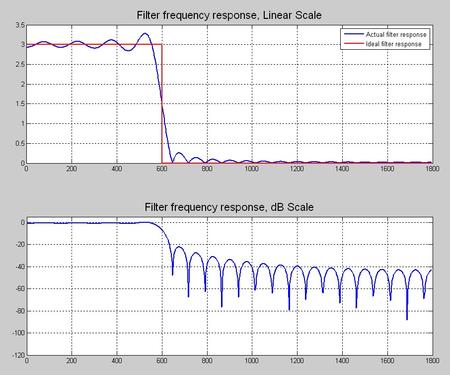
然后我们看看频域的幅频曲线，分别是线性尺度和dB尺度，我们看到这个滤波器的设计截止频率是900Hz，这符合公式的计算，而实现出来的滤波器的阻带衰减是-60dB左右。
插图，滤波器频响

接下来，看看全部信号的加窗DFT频谱，同样，可以看到，在900Hz的位置衰减到-60dB
插图，加窗DFT频谱

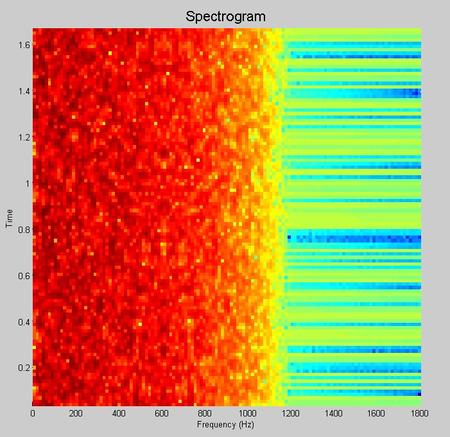
然后我们关注一下短时的幅频特性，元芳，上STDFT（短时傅里叶变换）频谱，然后讲讲你怎么看。
插图，瀑布图频谱

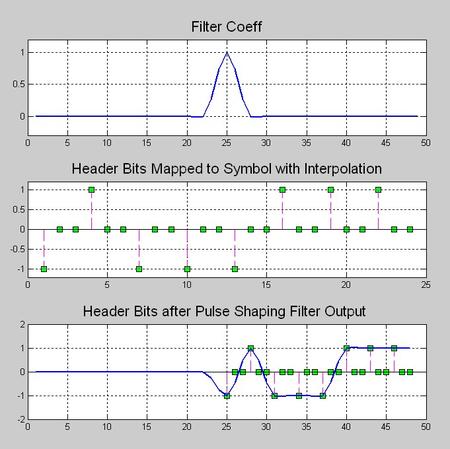
好，其它参数不变，我们改改滚降系数，首先是滚降系数为0的
插图，时域波形

砖墙是不可能完美实现滴，无限逼近吧，元芳，你看这个频谱，还记得信号与系统课本里面，有个词汇叫做“吉布斯现象”么？
注意看看滤波器的通带宽度和阻带衰减，惨不忍睹的-20dB啊
插图，滤波器频响

这信号带宽是600Hz，带外杂散很大。
插图，加窗DFT频谱

短时分析也是如此
插图，瀑布图频谱

接下来，再把滚降系数为改为1。
元芳，我大晚上写的烦躁，我妈喊我若干次赶紧睡觉了，你自己慢慢看吧。

插图，时域波形

插图，滤波器频响

插图，加窗DFT频谱

插图，瀑布图频谱

通信系统的确是复杂且零碎的一门学科，希望本文对您的学习能尽到绵薄之力，网络上曾有诗曰：

天若有情天亦老，人学通信死得早。
商女不知亡国恨，隔江犹看信息论。
问君能有几多愁，误码率都不会求。
两岸猿声啼不住，互相讨论谱密度。
忽如一夜春风来，信号流图不会排。
洛阳亲友如相问，直接去问韩声栋。
风萧萧兮易水寒，调制解调各种难。
垂死病中惊坐起，明天要考载噪比！

%///////////////////////////////////////////////////////////
% base band shaping use raised cosine FIR filter
%///////////////////////////////////////////////////////////
close all;
clear;
clc;

rate_symbol   = 1200                ; % input symbol rate
n_itp         = 3                   ; % num of interpolation
filter_delay  = 8                   ;
roll_off      = 1.0                 ;

head_bit      = [0 1 0 0 0 1 1 1 ].';
total_bit_len = 2048;
bit_map       = [-1 1]              ;

head_bit_len  = length(head_bit);
info_bit      = randint(total_bit_len-head_bit_len,1);

total_bit     = [head_bit; info_bit];

head_itp_len  = head_bit_len * n_itp;

fs_filter_out = n_itp*rate_symbol     % filter output sample rate

filter_delay_in_sample     = n_itp*filter_delay ;  

coeff = rcosine(rate_symbol, fs_filter_out, ... 
        'fir/normal', roll_off, filter_delay);

coeff       = coeff .'              ;

% map info_bit to multi-level signal
signal_1x       = bit_map(total_bit + 1) ;

len_1x          = length(signal_1x)     ;

len_itp         = len_1x * n_itp        ;
signal_itp      = zeros(len_itp,1)      ;
% write the original signal value into itp signal
signal_itp(1:n_itp:len_itp-n_itp+1) = signal_1x;

data_conv       = conv(coeff, signal_itp);
data_conv       = filter(coeff,1, signal_itp);
filter_out      = data_conv   ;

signal_itp_x_axis = [1:head_itp_len] + filter_delay*n_itp;

figure;
head_itp  = signal_itp(1:head_itp_len);
head_conv = data_conv(1:head_itp_len+filter_delay_in_sample);

subplot(3,1,1); plot(coeff, 'linewidth',1.5); grid on; ylim([-0.3, 1.2]);
title('Filter Coeff', 'FontSize', 16);

subplot(3,1,2); stem(head_itp,...
'--ms', 'MarkerEdgeColor','k','MarkerFaceColor','g', 'MarkerSize',6 );
title('Header Bits Mapped to Symbol with Interpolation', 'FontSize', 16);
ylim([-1.2, 1.2]);
grid on; 

subplot(3,1,3); stem(signal_itp_x_axis, signal_itp(1:head_itp_len), ...
'--ms', 'MarkerEdgeColor','k','MarkerFaceColor','g', 'MarkerSize',6 );
grid on; hold;
subplot(3,1,3); plot(head_conv, 'linewidth',1.5);grid on;
title('Header Bits after Pulse Shaping Filter Output ', 'FontSize', 16);

kaiser_beta     =  8    ;

kaiser_win_spectrum_plot(fs_filter_out, filter_out, kaiser_beta);
title('Total Signal Spectrum', 'FontSize', 16);

len_w = floor(total_bit_len /8);   
len_o = floor(len_w * 0.8);  
len_d = len_w    ;
figure  ;
% use tic toc get running time
spectrogram(filter_out, len_w, len_o, len_d, fs_filter_out);
title('Spectrogram', 'FontSize', 16);
% get filter frequency reponse vector over 0~pi
[f_rp_vec ,w_pi] = freqz(coeff); 
x_half_fs = w_pi/pi*(fs_filter_out/2);
f_rp_vec_norm_dB =  20*log10(abs(f_rp_vec)+1E-10);
f_rp_vec_norm_dB = f_rp_vec_norm_dB - max(f_rp_vec_norm_dB);

figure;
ideal_f_rp_vec = (x_half_fs < fs_filter_out/(2*n_itp))*n_itp;

subplot(2,1,1);
h1 = plot(x_half_fs, abs(f_rp_vec),  ...
x_half_fs, ideal_f_rp_vec, '-r', 'linewidth', 1.5);
grid on;

title('Filter frequency response, Linear Scale', 'FontSize', 16);
legend('Actual filter response', 'Ideal filter response');
subplot(2,1,2);
plot(x_half_fs, f_rp_vec_norm_dB, 'linewidth', 1.5);grid on;
title('Filter frequency response, dB Scale', 'FontSize', 16);
ylim([-120, 5]);

附件:

Matlab_Code_Base_Band_Pulse_Shaping.rar